FACTORISATION OF POLYNOMIALS
- If p(x) is a polynomial of degree n ≥ 1 and ‘a’ is a real then (x – a) is a factor of p(x) if p(a) = 0 and vice versa. This is called factor theorem.
- ax2 + bx + c is a quadratic polynomial where a, b, c are constants and a ¹ 0
For splitting the middle term method we split the co – efficient of x into two parts ‘m’ and ‘n’ such that b = m + n ….. a x c = m x n
- To factories ax2 + bx + c we have to write ‘b’ as the sum of two numbers
(m + n) and ac ‘as’ the product of those two numbers (m x n)
EXERCISE 2.4
- Determine which of the following polynomials has (x + 1) a factor:
Solution: (i) The zero of x + 1 is – 1
p(x) = x3 + x2 + x + 1
\p(-1) = (-1)3 + (-1)2 + (-1) + 1
= – 1 + 1 – 1 + 1
p(-1) = 0
When p(x) is divided by (x + 1) then the remainder is 0
Yes, (x + 1) is a factor of x3 + x2 + x + 1
(ii) The zero of x + 1 is – 1
p(x) = x4 + x3 + x2 + x + 1
p(-1) = (-1)4 + (-1)3 + (-1)2 + (-1) + 1
= +1 – 1 + 1 – 1 + 1
= 3 -2
p(-1) = 1 ¹ 0
The remainder is not zero
No, (x + 1) is not a factor of x4 + x3 + x2 + x + 1
(iii) The zero of (x + 1) is –1
p(x) = x4 + 3x3 + 3x2 + x + 1
\p (-1) = (-1)4 + 3(-1)3 + 3(-1)2 + (-1) + 1
= 1 + 3(-1) + 3(1) – 1 + 1
= 1 – 3 + 3 – 1 + 1
= 5 – 4
p(-1) = 1 ¹ 0
The remainder is not zero
No, (x + 1) is not a factor of x4 + 3x3 + 3x2 + x + 1
(iv) The zero of (x + 1) is – 1
p(x) = x3 – x2 – (2 + )x +
p(-1) = (-1) – (-1)2 – (2+ ) (-1) +
= -1 – (+ 1) – (-2 – ) +
= -1 – 1 + 2 + +
= -2 + 2 +
p(-1) = 2 ¹ 0
The remainder is not zero
No, (x + 1) is not a factor of x3 – x2 – (2 +
- Use the Factor Theorem to determine whether g(x) is a factor of p(x) in each of the following cases:
Solution: (i) g(x) = x + 1
The zero of (x + 1) is – 1
p(x) = 2x3 + x2 – 2x – 1
\p(-1) = 2(-1)3 + (-1)2 – 2(-1) – 1
= 2(-1) + (1) + 2 – 1
= -2 + 1 + 2 – 1
p(-1) = 0
Since p(x) = 0
Yes, g(x) is a factor of p(x)
(ii) g(x) = x + 2
The zero of x + 2 is – 2
p(x) = x3 + 3x2 + 3x + 1
p(-2) = (- 2)3 + 3(- 2)2 + 3 (- 2) + 1
= (- 8) + 3(4) – 6 + 1
= – 8 + 12 – 6 + 1
= 13 – 14
p(-2) = -1 ¹0
Since p(x) ¹ 0
No g(x) is not a factor of p(x)
(iii) g(x) = x – 3
The zero of x – 3 is 3
p(x) = x3 – 4x2 + x + 6
p(3) = (3)3 – 4(3)2 + 3 + 6
= 27 – 4(9) + 9 = 27 – 36 + 9 = 36 – 36
p(3) = 0
Since p(x) = 0
Yes, g(x) is a factor of p(x)
- Find the value of k, if x–1 is a factor of p(x) in each of the following cases:
Solution : (i) The zero of x – 1 is 1
For (x – 1) to be a factor of P(x)
p(1) must be 0
p(x) = x2 + x + k
p(1) = (1)2 + 1 + k
= 2 + k
2 + k = 0
k = – 2
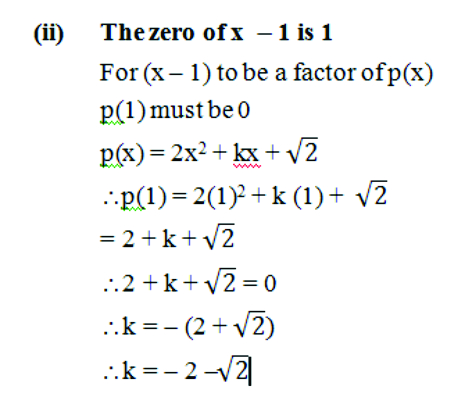
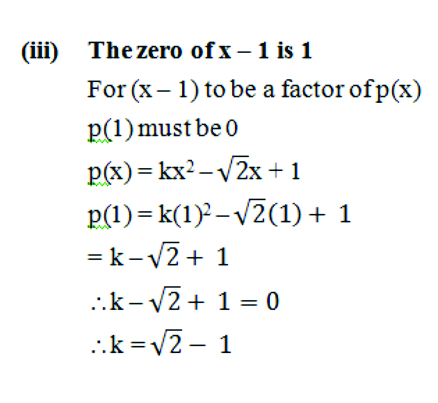

- Factorize: (i) 12x2 – 7x + 1
Solution: Using the splitting the middle term method,
We have to find a number whose sum = -7 and product =1 × 12 = 12
We get – 3 and – 4 as the numbers [(-3) + (- 4)] = -7 and [- 3 × – 4 = 12]
12x2 – 7x + 1 = 12x2 – 4x – 3x + 1
= 4x(3x – 1) – 1(3x -1)
= (4x – 1) (3x – 1)
- ii) 2x2 + 7x + 3
Comparing it with ax2 + bx + c we get a = 2, b = 7, c = 3
(m + n) = 7 and m x n = a x c = 2 x 3 = 6
The two numbers m and n are 6, 1
2x2 + 7x + 3
= 2x2 + 6x + x +3
= 2x (x + 3) + 1 (x + 3)
= (x + 3) (2x + 1)
The factors of 2x2 + 7x + 3 are (x + 3) (2x + 1)
iii). 6x2 + 5x – 6
Comparing it with ax2 + bx + c we get a = 6, b = , c = 6
(m + n) = 5 and m x n = a x c 6 x c – 6 = – 3
The two numbers m and n are + 9, – 4
6x2 + 5x – 6
= 6x2 + 9x – 4x – 6
=3x (2x + 3) – 2 (2x + 3)
= (2x + 3) (3x – 2)
The factors of 6x2 + 5x – 6 are (2x + 3) (3x – 2)
- Factorize:
Solution: (i). p(x) = x3– 2x + x + 2
The possible factors are +1, -1, + 2, -2 etc
p(1) – (1)3 – 2 (1)2 – (1) + 2
= 1 -2 – 1 + 2
p(1) = 0
x = 1 is a factor of p(x) it means (x -1) is factor of x3 – 2x2 – x + 2
One factor is (x – 1) we can find the other two factors of x2 – x – 2
by splitting the middle term method
x2 – x + 2
= x2 – 2x + x – 2
= x(x – 2) + 1 (x – 2)
= (x – 2) (x + 1) are the other two factors
\the three factor are (x – 1) (x – 2) and (x + 1)
(ii) p(x) = x3 – 3x2 – 9x – 5
The possible factors are +1, -1, + 2, -2 etc
\p(1) = (1)3 – 3(1)2 – 9 (1) – 5
= 1 – 3 – 9 – 5 = -18
\p(1) = -18 ¹ 0
Now consider p (-1) = (–1)3 – 3(-1)2 – 9 (-1) – 5
= (-1) – 3 (1) + 9 – 5
= – 9 + 9 = 0
\p(-1) – 0
It means that (x + 1) is a factor of p(x)
Now factories the quotient x2 – 4x – 5 to find the other two factors
x2 – 4x – 5
= x2 – 5x + x – 5
= x(x – 5) + 1 (x – 5)
= (x – 5) (x+ 1) are the other two factors
\The 3 factors are (x + 1) (x + 1) (x – 5)
(iii) p(x) = x3 + 13x2 + 32x + 20
The possible factors are +1, – 1, + 2, – 2 etc
p(1) = (1)3 + 13(1) + 32(1) + 20
= 1 + 13 + 32 + 20
\p(1) = 66 ¹ 0
Then consider
p (-1) = (-1)3 + 13(-1)2 + 32(-1) + 20
= -1 + 13 – 32 + 20
= 33 – 33
\p(-1) = 0
It means that (x + 1)is a factor of p(x)
Now factories x2 + 12x + 20 to get the other factors
x2 + 12x + 20
= x2 + 10x + 2x + 20
= x (x + 10) + 2 (x + 10)
= (x + 10) (x + 2) are the other two factors
\the 3 factors are (x + 1)(x + 2)(x + 10)
(iv) p(y) = 2y3 + y2 – 2y – 1
The possible factors are +1, -1, +2, -2…..
P(1) = 2(1)3 + (1)2– 2 (1) – 1
= 2 + 1 – 2 – 1
\p(1) = 0
It means that (y – 1) is a factor of p(y)
Now factoris 2y2 + 3y + 1 to get the other factors
2y2 + 3y +1 = 2y2 + 2y + y + 1
= 2y (y + 1) + (y + 1)
= (y + 1) (2y + 1) are the other two factors
\the three factors are (y – 1 ) (y + 1) 2y

