ALGEBRAIC IDENTITIES
1. (x + y)2 = x2 + 2xy + y2
2. (x –y)2 = x2 – 2xy + y2
3. x2 – y2 = (x + y) (x – y)
4. (x + a) (x + b) = x2 + (a + b) x + ab
5. (x + y + z)2= x2 + y2 + z2 + 2xy + 2yz + 2zx
6. (x + y)3 = x3 + y3 + 3xy (x + y) or x3 + y3 + 3x2y + 3xy2
7. (x – y)3 = x3 – y3 – 3xy (x – y) or x3 – y3 – 3x2y + 3xy2
8. x3 + y3 + z3 – 3xyz = (x + y + z) (x2 + y2 + z2 – xy – yz – zx)
9. x3 + y3= (x + y) (x2 –xy + y2)
10. x3 – y3= (x – y) (x2 + xy + y2)
EXERCISE 2.5
1. Use suitable identities to find the following products:
Solution: (i) (x + 4) (x + 10)
(Using identity: (x + a) (x + b) = x2 + (a + b) x + ab)
Here a = 4 , b = 10
(x + 4) (x + 10)
= x2 + (4 + 10) x + (4 x 10)
= x2 + 14x + 40
The product is x2 + 14x + 40
(ii) (x + 8) (x – 10)
Using identity:
(x + a) (x + b) = x2 + (a + b) x + ab
Here a = 8 b = -10
(x + 8) (x – 10) = x2 + (8 – 10) x + 8 (-10)
= x2-2x – 80
The product is x2 – 2x – 80
iii) (3x+ 4) (3x – 5)
Using identity:
(x + a) (x + b) = x2 + (a + b) x + ab
Here x = 3 a = 4, b = – 5
(3x + 4) (3x – 5) = (3x)2 + (4 – 5) 3x + (4) (-5)
= 9x2 – 3x – 20
The product is 9x2 – 3x – 20
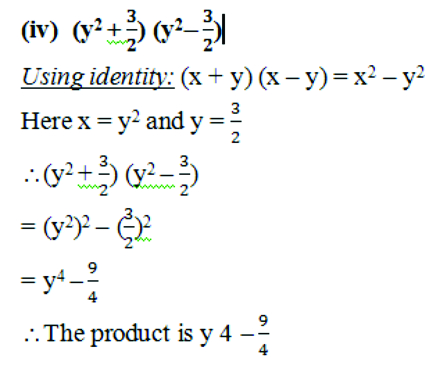
- v) (3 – 2x) (3 + 2x)
Using identity: (x + y) (x – y) = x2 – y2
Here x = 3, y = 2x
(3 – 2x) (3 + 2x) = (3)2 – (2x)2
= 9 – 4x2
The product is 9 – 4x2
2. Evaluate the following products without multiplying directly:
Solution: i) 103 x 107
103 = (100 + 3) and 107 = (100+7 )
Use identity: (x + a) (x + b) = x2 + (a + b) x + ab
Here x = 100, a = 3, b = 7
(100 + 3) (100 + 7) = (100)2 + (3 + 7)100 + (3) (7)
= 10000 + 1000 +21
= 11021
The product of 13 x 107 is 11021
ii) 95 x 96
Method 1.
95 = 100 – 5, 96 = 100- 4
Use identity; (x + a) (x+ b) = x2 + (a + b) x + ab)
Here a= – 5, b = -4, x = 100
(100 – 5) (100 – 4) = (100)2 + (-5-4)100 + (– 5) (– 4)
= 10000 – 900 + 20
= 9120
The product of 95 x 96 = 9120
Method 2:
95 = 90 + 5 96 = 90 + 6
Use identity: (x + a) (x + b) = x2 + (a + b) x + ab
Here x = 90, a = 5, b = 6
(90 + 5) (90 + 6) = (90)2 + (5 + 6) 90 + (5) x (6)
= 8100 + 990 +30
= 9120
The product of 95 x 96 is 9120
iii) 104 x 96
104 = 100 + 4, 96 = 100 – 4
Use identity: (x + y) (x – y) = x2 – y2
Here x = 100, y = 4
(100 + 4) (100 – 4) = (100)2 – (4)2
= 10000 – 16
= 9984
The product of 104 x 96 = 9984
3. Factorize the following using appropriate identities:
Solution: (i) 9×2 + 6xy + y2
(Since it has 3 terms and squares and plus sign)
Identity: a2 + 2ab + b2 = (a + b)2
9×2 + 6xy + y2 a = 3x, b = y
= (3xy)2 + 2 (3x) (y) + (y)2
= (3x + y)2 = (3x + y) (3x + y)
- ii) 4y2 – 4y + 1
(It has squares and 3 terms and minus sign)
4y2 – 4y + 1
Identity: is a2– 2ab + b2 = (a – b)2
= (2y)2 – 2(2y) (1) + (1)2
= (2y – 1)2
= (2y – 1) (2y – 1)
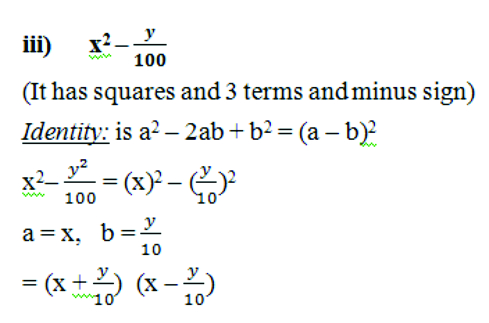
(i) (x + 2y + 4z)2
(It has 3 terms and (bracket)2
Identity: is (a + b + c)2 = a2 + b2 +c2 +2ab + 2bc+ 2ca
Here a = x, b = 2y, c = 4z
(x + 2y + 4z)2
= (x)2 + (2y)2 + (4z)2 + 2(x) (2y) + 2 (2y)(4z) + 2 (4z)(x)
= x2 + 4y2 + 16z2 + 4xy + 16yz + 8zx
- ii) (2x – y + z)2
Identity: (a + b + c)2 = a2 + b2 +c2 + 2ab + 2bc + 2ca
Here a = 2x, b = –y, c = z
\(2xy – y + z)2
= (2x)2 + (–y)2 + (z)2 + 2(2x) (-y) + 2(-y) (z) + 2(z) (2x)
= 4x2 + y2 + z2 – 4xy – 2yz + 4xz
iii) (– 2x + 3y + 2z)2
Identity : (a + b + c)2 = a2 + b2 + c2 + 2ab +2bc + 2ca
Here a = – 2x, b = 3y, c =2z
\(- 2x + 3y + 2z)2
= (- 2x)2 + (3y)2 + (2z)2 + (2) (- 2x) (3y) + 2(3y)(2z) + 2(22) (- 2x)
= 4x2 + 9y2 + 4z2 – 12xy + 12yz – 8xz
(iv) (3a – 7b – c)2
Identity : (a + b + c)2 = a2 + b2 + c2 + 2ab + 2bc + 2ca
Here a = 3a, b = -7b, c = – c
\(3a – 7b – c)2
= (30)2 + (-7b)2 + (-c)2 + 2(3a) (-7b) + 2(-7b)(-c) + 2(- c)(3a)
= 9a2 + 49b2 + c2 – 42ab + 14bc – 6ac
(v) (–2x + 5y – 3z)2
Identity: (a + b + c)2 = a2 + b2 + c2 + 2ab + bc + 2ca
Here a = 2x, b = 5y, c = – 3z
(2x + 5y – 3z)2
= (- 2x)2 + (5y)2 + (- 3z)2 + 2(- 2x)(5y) + 2 (5y)(- 3z) + 2(- 3z)(- 2x)
= 4x2 + 25y2 + 9z2 – 20xy – 30yz + 12xz
(iv) (3a – 7b – c)2
Identity : (a + b + c)2 = a2 + b2 + c2 + 2ab + 2bc + 2ca
Here a = 3a, b = -7b, c = – c
\(3a – 7b – c)2
= (30)2 + (-7b)2 + (-c)2 + 2(3a) (-7b) + 2(-7b)(-c) + 2(- c)(3a)
= 9a2 + 49b2 + c2 – 42ab + 14bc – 6ac
(v) (–2x + 5y – 3z)2
Identity: (a + b + c)2 = a2 + b2 + c2 + 2ab + bc + 2ca
Here a = 2x, b = 5y, c = – 3z
\(2x + 5y – 3z)2
= (- 2x)2 + (5y)2 + (- 3z)2 + 2(- 2x)(5y) + 2 (5y)(- 3z) + 2(- 3z)(- 2x)
= 4x2 + 25y2 + 9z2 – 20xy – 30yz + 12xz
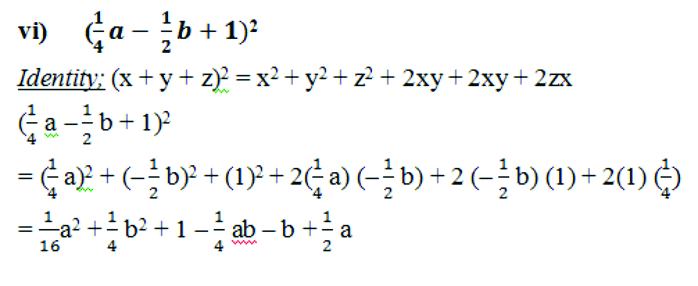
5. Factorize:
(i) (2x + 1)3
It has 2 terms and (bracket)3
Identity: (a + b) = a3 + b3 + 3ab (a + b)
Here a = 2x b = 1
(2x + 1)3 = (2x)3 + (1) + 3(2x) (1) (2x + 1)
=8x3 + 6x (2x + 1)
= 8x3 + 1 + 12x2 + 6x
= 8 x3 + 12x2 + 6x + 1
(2a = 3b)3
It has two terms and ( )3
Identity: (x + y)3 = x3 – y3 – 3xy (x – y)
Here x = 2a , y = 3b
(2a – 3b)3
= (2a)3 – (3b)3 – (3) (2a) (3b) (2a – 3b)
= 8a3 – 27b3 – 18ab (2a – 3b)
= 8a3 – 27b3 – 36a2b + 54ab2
6. Write the following cubes in expanded form:
Solution: (i) (2x + 1)3
It has 2 terms and (bracket)3
Identity: (a + b) = a3 + b3 + 3ab (a + b)
Here a = 2x b = 1
(2x + 1)3 = (2x)3 + (1) + 3(2x) (1) (2x + 1)
=8×3 + 6x (2x + 1)
= 8×3 + 1 + 12×2 + 6x
= 8 x3 + 12×2 + 6x + 1
ii) (2a = 3b)3
It has two terms and ( )3
Identity: (x + y)3 = x3 – y3 – 3xy (x – y)
Here x = 2a , y = 3b
(2a – 3b)3
= (2a)3 – (3b)3 – (3) (2a) (3b) (2a – 3b)
= 8a3 – 27b3 – 18ab (2a – 3b)
= 8a3 – 27b3 – 36a2b + 54ab2
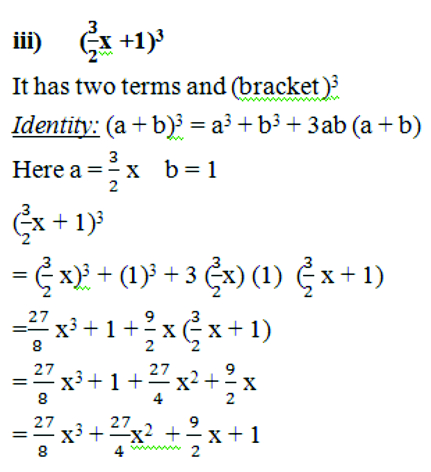
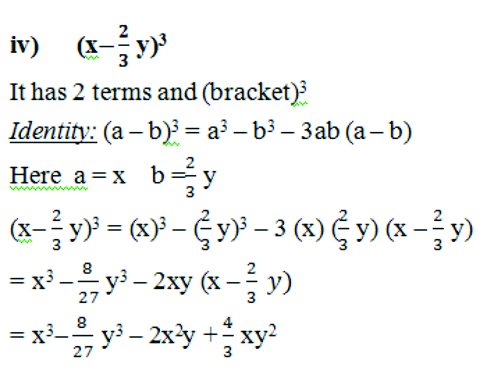
7. Evaluate the following using suitable identities:
Solution: (i) (99)3
(99)3 = (100- 1)3
Identity: (x – y)3 = x3 – y3 – 3xy (x –y)
Here x = 100, y = 1
(99)3 = (100 – 1)3
= (100)3 – (1)3 – 3 (100) (1) (100 – 1)
= 1000000 – 1 – 300 (99)
= 1000000 – 1 – 29700
= 1000000 – 29701 = 9702999
(99)3 = 970299
ii) (102)3
(102)3 = (100 + 2)3
Identity:(x + y)3 = x3 + y3 + 3xy (x + y)
Here x = 100 y = z
(100 + 2)3 = (100)3 + (2)3 + (3) (100) (2) (100 + 2)
= 1000000 + 8600 (102)
= 1000008 + 61200
= 1061208
(102)3 = 1061208
iii) (998)3
(998)3 = (1000 – 2)3
Identity: (x-y)3 = x3– 43-3xy (x-y)
Here x = 1000 y = 2
(1000-1)3
= (1000)3 – (2)3 – 3(1000) (1) [1000 – 1]
= 1000000000 – 8 – 3000(999)
= 1000000000 – 2997008
= 994011992
- Factories each of the following:
Solution: (i) 8a3 + b3 + 12a2b + 6ab2
(It is a cube sum and it has 4 terms)
Identity: (x + y)3 = x3 + y3 + 3x2y + 3xy2
Here x = 3 = 2a y = 3
8a3 + b3 + 12a2 + 6ab2
= (2a)3 + (b)3 + 3 (2a)2 (b) + 3(2a) (b)2
= (2a + b)3
= (2a +b) (2a + b) (2a +b)
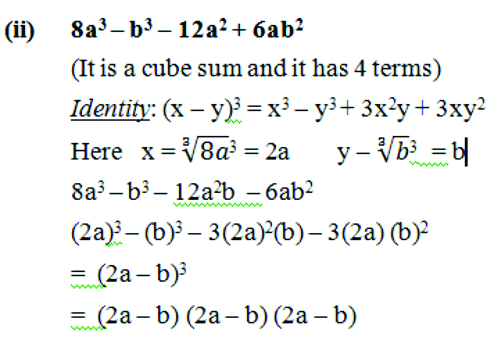
(iii) 27 –125a3 – 135a + 225a2
(It is a cube sum with 4 terms)
Identity :(x – y)3 = x3 – y3 – 3x2y + 3xy2
Here x = = 3 y = 3 = 5a
\ 27 – 125a3 – 135a + 225a2
= (3)3 – (5a)3 – 3(3)2 (5a) + 3(3) (5a)2
= (3 – 5a)3
= (3 – 5a) (3 – 5a) (3 – 5a)
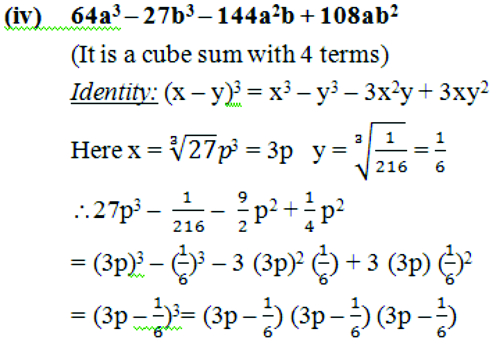
- Verify:
Solution:
(i) x3 + y3 = (x + y) (x2 – xy – y2)
= x (x2 – xy + y2) + y (x2 – xy + y2)
= (x3 – x2y + xy2) + (x2y – xy2 + y3)
= x3 – x2y + xy2 + x2y – xy2 + y3
= x3 – y3
L. H. S = R. H. S
(ii) x3 – y3 = (x- y) (x2 + xy + y2)
= x (x2 + xy + y2) – y (x2 + xy + y2)
= (x3 + x2y + xy=) – (x2y + xy2 + y3)
= x3 + x2y + xy2 – x2y – xy2 – y3
= x3 – y3
\L. H. S = R. H. S
- Factorize each of the following:
Solution: i) 27y3 + 125 z3
= (3y)3 + (5z)3
Identity:a3 + b3 = (a + b) (a2 – ab + b2)
Here a = 3y, b = 5z
(3y)3 + (5z)3
= (3y + 5z) [(3y)2 – (3y) (5z) + (5z)2]
=(3y + 5z) (9y2 – 15yz + 25z2)
- ii) 64m3 – 343n3
= (4m)3 – (7n)3
Identity: a3 – b3 = (a – b) (a2 + ab + b2)
Here a = 4m, b = 7n
(4m)3 – (7n)3
= (4m – 7n) [(4m)2 + (4m) (7n) + (7n)2]
= (4m – 7n) (16m2 + 28mn + 49n2)
- Factories: 27x3 + y3 + z3 – 9xyz
Solution: 27x3 + y3 + z3 – 9xyz
(It is a cube sum and 4 terms)
Identity: a3 + b3 + c3 – 3abc = (a + b + c) (a2 + b2 + c2) – ab – bc – ca
27x3 + y3 + z – 9xyz
= (3x)3 + (y)3 + (z)3 – 3 (3x) (y) (z)
Here a = 3x, b = y, c = z
\ 27x3 + y3 – 23 – 9xyz
= (3x + y + z) [(3x)2 + (y)2 + (z)2 – (3x)(y) – (y)(z) – (z) (3x)]
= (3x + y + z) (9x2 + y2 + z2 – 3xy – yz – 3xz)
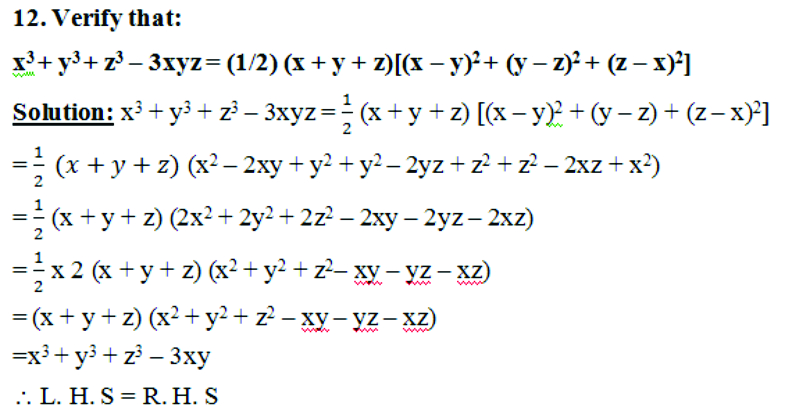
- If x + y + z = 0, show that x3 + y3 + z3 = 3xyz.
Solution: Method 1:
The identity is
x3 + y3 + z3 – 3xyz = (x + y + z) (x2 + y2 + z2 – xy – yz – zx)
= (0) (x2 + y2 + z2 – xy – yz – zx)
(x + y + z) = 0 given)
\x3 + y3 + z3 – 3xyz = 0
x3 + y3 + z3 = 3xyz
Method 2:
Given x + y + z = 0
x + y = – z
Cubing both sides we get
(x + y)3 = (-z)3
x3 + y3 + 3xy 9x+ y) = -z3
x3 + y3 + 3xy (-z) = -z3
x3 + y3 – 3 xyz = -z3
\x3 + y3 = -z3 + 3xyz
\x3 + y3 + z3 = 3xyz
- without actually calculating the cubes, find the value of each of the following:
Solution: (i) (–12)3 + (7)3 + (5)3
Let x = – 12, y = 7, z = 5
Now x + y+ z = (-12) + 7 + 5 = 0
If, x + y +z = 0
Then x3 + y3 + z3 = 3xyz
\ (-12)3 + (7)3 + (5) + = 3 (-12) (7) (5)
= (-12) (105)
= -1260
\ (-12)3 + (7)3 + (5)3= -1260
- ii) (28)3 + (–15)3 + (–13)3
Let x = 28, y = –15, z = -13
Now x + y + z = 28 – 15 – 13 = 0
If x + y +z = 0
Then x3 + y3 + z3 = 3xyz
(28)3 + (-15)3 + (-13)3 = 3 (28) (-15) (-13)
= (- 45) x -364
= 16380
\ (28)3 + (-15)3 + (-13)3 = 16380
- Give possible expressions for the length and breadth of each of the following rectangles, in which their areas are given:
Solution: (i) Area = 25a2 – 35a + 12
We know that Area = length x breadth
(We have to factories the area)
25a2 – 35a + 12
25a2 – 15a – 20a + 12
5a (5a – 3) – 4 (5a – 3)
(5a – 3) (5z – 4)
\The length could be (5a – 3) and the breadth could be (5a – 4)
(ii). Area = 35y2 + 13y – 12
(Area = length x breadth)
35y2 + 13y – 12
35y2 + 28y – 15y – 12
7y (5y + 4) – 3 (5y + 4)
(5y + 4) (7y – 3)
The possible length is (7y – 3) and the possible breadth is (5y + 4)
- What are the possible expressions for the dimensions of the cuboids whose volumes are given below.
(i) Volume: 3x2 – 12x
(ii) Volume: 12ky2 + 8ky – 20k
Solution :( i) Volume: 3x2 – 12x
Volume of cuboid = length x breadth x height
Factorizing 3x2 – 12x
= 3x (x – 4)
= (3) (x) (x – 4)
The possible dimensions are 3, (x), (x – 4) units
- ii) Volume = 12ky2 + 8ky – 20k
Volume of cuboid = length x breadth x height
Factorising 12ky2 + 8ky -20k
= 4k (3y2 + 2y – 5)
= 4k(3y2 + 5y – 3y – 5)
= 4k [y (3y + 5) – 1(3y + 5)]
= (4k)(3y + 5) (y – 1)
\The possible dimensions are (4k), (3y + 5) and (y – 1)

