6.4 LINES PARALLEL TO THE SAME LINE:
* Each pair of interior opposite angles are supplementary ( equal to 1800 )
EXERCISE 6.2
1 ) In Fig. 6.28 find the values of x and y and then show that AB ∥ CD
Given : ∠PEA = 50° and ∠CFQ = 130°
To find: ( i ) value of x and y
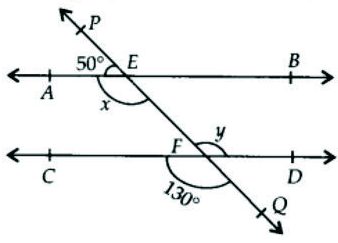( ii ) Show that AB ∥ CD.
Proof : ( i ) ∠ y = 130° ( vertically opposite angles )
∴ y = 130°
∠ x + 50° = 180° ( linear pair )
∴ ∠ x = 180° − 50° ⇒ ∠ x = 130°
∴ x = 130°
( ii ) We know that ∠ x = ∠ y = 130°
They are alternate interior angles and they are equal.
So by Theorem 6.3
If a transversal intersects two lines such that a pair of alternate
interior angles are equal then the two lines are parallel
∴ AB ∥ CD
2 ) In Fig. 6.29, if AB ∥CD , CD ∥ EF and y ∶ z = 3 ∶ 7, find x.
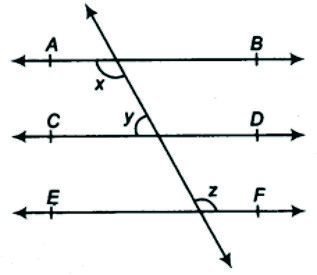
Given :
AB ∥ CD, CD ∥ EF
And y ∶ z = 3 ∶ 7
To find : value of x
∠ x = ∠ y ( vertically opposite angles )
Proof : From Theorem 6.4 it states that if a transversal intersects
two parallel lines then each pair of interior angles on the
same side of the transversal is supplementary.
∴ ∠ y + ∠ z = 180°
The ratio y ∶ z is 3 ∶ 7
Let the multiplicative value of the ratio be x.
∴ y = 3 x and z = 7 x ⇒ 3 x + 7 x = 180°
10 x = 180° ⇒ x = 18°
∴ y = 3 x = 3 x 18° = 54° ⇒ y = 54°
z = 7 x = 7 x 18° = 126° ⇒ z = 126°
3 ) In Fig. 6.30, if AB ∥ CD, EF ⊥ CD and ∠ GED = 126°, find ∠ AGE, ∠ GEF and ∠ FGE.
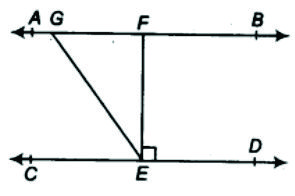Given: AB ∥ CD, EF ⊥ CD and ∠ GED = 126°
To find : ∠ AGE, ∠ GEF and ∠ FGE
Proof : ( i ) Since EF ⊥ CD we get
∠ CEF = ∠ FED = 90°
Also ∠ GED = ∠ GEF + ∠ FED
∴ ∠ GED = ∠ GEF + 90° (∠ FED = 90°)
1260 = ∠ GEF + 90° (∠ GED = 126°)
∴ ∠ GEF = 36°
( ii ) Now ∠ AGE = ∠ GED ( interior opposite angles are equal )
∴ ∠ AGE = 126°
( iii ) ∠ AGE + ∠ FGE = 180° ( linear pair )
∴ 126° + ∠ FGE = 180°
∴ ∠ FGE = 54°
4 ) In Fig. 6.31, if PQ ∥ ST, ∠ PQR = 110° and ∠ RST = 130°, find ∠ QRS.
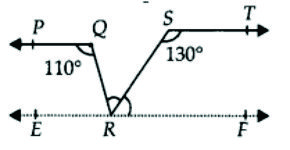Given: ∠ PQR = 110° ∠ RST = 130° and PQ ∥ ST
To find : ∠ QRS = ?
Const: Draw XY ∥ PQ ∥ ST passing through point R
Proof: ( i ) Now PQ ∥ XR ( by construction )
Interior angles on the same side of the transversal
QR is supplementary
∴ ∠ PQR + ∠ QRY = 180°
110° + ∠ QRY = 180°
∴ ∠ QRY = 180° – 110° = 70°
( ii ) Again ST ∥ RY
Interior angles on the same side of the transversal QR is supplementary
∴ ∠ TSR + ∠ SRX = 180°
130° + ∠ SRX = 180°
∴ ∠ SRX = 180° – 130° = 50°
( iii ) XRY is a straight line
∠ QRY + ∠ QRS + ∠ SRX = 180°
70° + ∠ QRS + 50° = 180°
120° + ∠ QRS = 180°
∴ ∠ QRS = 60°
5 ) In Fig 6.32, if AB ∥ CD, ∠ APQ = 50° and ∠ PRD = 127°, find x and y.
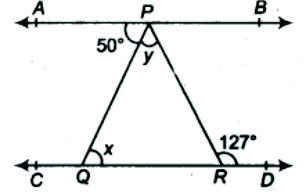
Given: AB ∥ CD ∠ APQ = 50° and ∠ PRD = 127°
To find: x and y
Proof : ( i ) Since AB ∥ CD
∠ APQ = ∠ PQR ( interior opposite angles )
∴ 50° = ∠ PQR ⇒ ∠ PQR = x = 50°
∴ x = 50°
( ii ) ∠ x + ∠ y = 127°
( external angle is equal to sum of interior opposite angles )
50° + ∠ y = 127°
∴ ∠ y = 127° − 50°
∴ ∠ y = 77°
6 ) In Fig. 6.33, PQ and RS are two mirrors placed parallel to each other. An incident ray AB
strikes the mirror PQ at B, the reflected ray moves along the path BC and strikes the
mirror RS at C and again reflects back along CD. Prove that AB ∥ CD.
Given : PQ and RS are two mirrors placed parallel to each other
Const:Draw BE perpendicular to PQ and draw CF perpendicular to RS
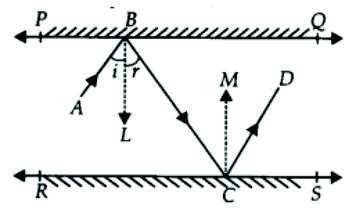To prove : AB ∥ CD.
Proof : We know that
angle of incidence = angle of reflection ( laws of reflection )
∴ ∠ ABE = ∠ EBC = x – – – – – – ( 1 )
And ∠ BCF = ∠ FCD = y – – – – – ( 2 )
Also BE ⊥ PQ, CF ⊥ RS and PQ ∥ RSx
We get BE ∥ CF
Now BE∥ CF and BC is transversal
∠ EBC = ∠ BCF ( alternate interior angles )
x = y ⇒ 2 x = 2 y ( Multiply both sides by 2 )
∠ ABC = ∠ BCD
These are alternate interior angles and since they are equal so the lines are parallel
Hence AB ∥ CD