6.6 ADDITIONAL QUESTIONS:
1. Lines AB and CD intersect each other at point O If ∠ AOD ∶ ∠ BOD = 4 ∶ 5, Find all the angles
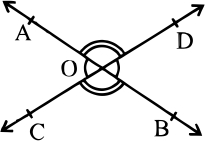
Method 1: Let the angle measure be ‘x’
( we are given the ratio 4 ∶ 5 which will become 4 x and 5 x )
We know that ∠ AOD + ∠ BOD = 180° ( linear pair )
∴ 4 x + 5 x = 180° ⇒ 9 x = 180° ⇒ x = 20°
∴ 4 x = 4 x 20° = 80° = ∠ AOD
∴ 5 x = 5 x 20° = 100° = ∠ BOD
But ∠ AOC = ∠ BOD ( vertically opposite angles are equal )
∴ ∠ AOC = 100°
And ∠ AOD = ∠ BOC ( vertically opposite angles are equal )
∴ ∠ BOC = 80°
So we get ∠ AOD = ∠ BOC = 80°
And ∠ AOC = ∠ BOD = 100°
Method 2: We know that ∠ AOD + ∠ BOD = 180° ( linear pair )
And ∠ AOD ∶ ∠ BOD = 4 ∶ 5 ( given )
∴ ∠ AOD = 4/9 x 18° ( 5 + 4 = 9 )
∴ ∠ AOD = 80°
Now ∠ AOD = ∠ BOC ( vertically opposite angles are equal )
∴ ∠ BOC = 80°
Similarly we know that ∠ AOD + ∠ BOD = 180° ( linear pair )
And ∠ BOC = 80° ( already proved )
∴ ∠ AOC + 80° = 180*
∴ ∠ AOC = 180° – 80° = 100°
And ∠ AOC = ∠ BOD ( vertically opposite angles are equal )
∴ ∠ BOD = 100°
∴We get ∠ AOD = ∠ BOC = 80°
And ∠ AOC = ∠ BOD = 100°
2. In the fig. Ray OD stands on the line AOB. Rays OC and OE are the angle bisectors of ∠ AOD and ∠ BOD respectively. If ∠ AOD = x find ∠ COE.
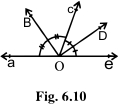
Solution: Ray OD stands on the line AOB so we get
∠ AOD + ∠ BOD = 180° ( linear pair )
∴ x + ∠ BOD = 180° ( ∵ ∠ AOD = x )
∴ ∠ BOD = 180° – x
Now ray OC bisects ∠ AOD
∴ we get ∠ COD = ½ ∠ AOD = ½ x
∴ ∠ COD = ½ x
Similarly ray OE bisects ∠ BOD
∠ DOE = ½ ∠ BOD
∴ ∠ DOE = ½ ( 180° – x )
Now we know that
∠ COE = ∠ COD + ∠ DOE ( from the fig )
Putting these values from above we get
∠ COE = x/2 + 1/2 ( 180° – x )
= x/2 + 90° − x/2 ⇒ ∠ COE = 90°
6 ) PQ ∥ RS ∥ MN. Also MP ⊥ PQ
If ∠ QMN = 60°. Find the values of x, y, z
Solution: i ) Consider RS ∥ MN
Here MS becomes the transversal.
∴ y + 60° = 180°°
( because interior angles on the same side of the transversal are supplementary )
∴ y = 180° – 60°
∴ y = 120°
ii ) Now consider PQ ∥ RS and BD is the transversal z = y
( corresponding angles are equal )
∴z = 120°
iii ) Since PQ ∥ RS and RS ∥ MN we have PQ ∥ MN
MP is the transversal
∠ MPQ + ∠ NMP = 180°
( Interior angles on the same side of the transversal
are equal )
90° + x + 60° = 180°
150° + x = 180° x = 180° – 150°
∴ x = 30°
7 ) Prove that the sum of the angles of a triangle is 180.
Given: PQR is a triangle ( 4 ) x ( 5 )
To prove: ∠ 1 + ∠ 2 + ∠ 3 = 180°
Const:Draw line XPY
Proof: Now since XPY is a line we get
∠ 4 + ∠ 1 + ∠ 5 = 180° – – – – – – – – – –
( Angles on a straight line is 180° )
Line XPY ∥ QR
And PQ is the transversal
∠ 4 = ∠ 2 ( alternate interior angles ) – – – – – – – – – –
( Alternate interior angles are Z shaped )
Again XPY ∥ QR
And PR is the transversal
∠ 3 = ∠ 5 ( alternate interior angles ) – – – – – – – – –
Substituting the value of ( 2 ) and ( 3 ) in ( 1 )
We get
∠ 4 + ∠ 1 + ∠ 5 = 180°
∠ 2 + ∠ 1 + ∠ 3 = 180° ( ∵ ∠ 4 = ∠ 2 , ∠ 5 = ∠ 3 )
∴ ∠ 1 + ∠ 2 + ∠ 3 = 180°
8 ) In Fig. PQ ∥ ST
∠ QPR = 50° and ∠ RST = 70°, find ∠ SRT. Given: ∠ QPR = 50° and ∠ RST = 70° To find: ∠ SRT. = ?
Proof: PQ ∥ ST and PT is the transversal
∴ ∠ QPR = ∠ RTS ( alternate interior angles )
∠ RTS = 50° ( ∵ ∠ QPR = 50° given )
PQ°
Consider ⊿RST500
∠ RST + ∠ RTS + ∠ SRT = 180°
70° + 50° + ∠ SRT = 180°
120° + ∠ SRT = 180°
∴ ∠ SRT = 180* – 120° = 60° 70°
( 9 ) In the fig. if AB⊥AD and AB ∥DE
∠ DBC = 40° and
∠ BCE = 70° find the values of x and y
Solution: Since AB ∥ DE and BC is the transversal
We get ∠ ABC = ∠ BCE ( alternate interior angles )
x + 40° = 70° ( since ∠ ABC = x + 40° and ∠ BCE = 70° given )
∴ x = 70° – 40°
∴x = 30°
Now consider ∆ ADB
∠ ADB + ∠ DBA + ∠ DAB = 180° ( Angles of a triangle is 180* )
y + x + ∠ DAB = 180° – – – – – – – – – – – – ( 1 )
( But x = 30° proved above )
∠ DAB = 90° since AB ⊥AD
Putting these values in ( 1 ) we get
y + 30° + 90° = 180°
y + 120° = 180° y + 30° + 90° = 180°
y + 120° = 180°
y = 180° – 120°
y = 60°
∴ The values are x = 30°, y = 60* proved
3 ) Transversal and All Angles:
( i ) Corresponding Angles:
( a ) ∠1 and ∠5 ( b ) ∠2 and ∠6
( c ) ∠4 and ∠8 ( d ) ∠3 and ∠7
Just add the value 4 to the angle and you will get the corresponding angle
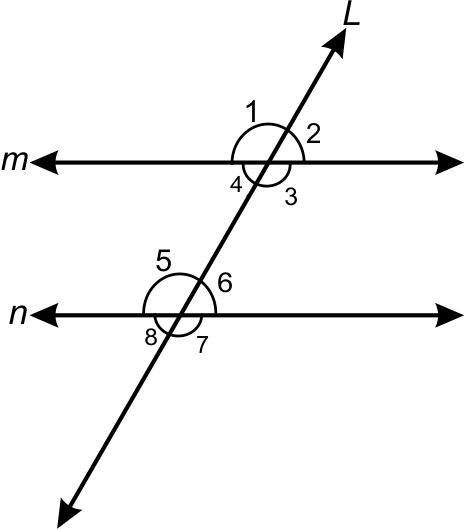
Also remember 1 + 4 = 5
So ∠ 1 and ∠ 5 } And 2 + 4 = 6
So ∠ 2 and ∠ 6 } And 3 + 4 = 7
So ∠ 3 and ∠ 7 } And 4 + 4 = 8
So ∠ 4 and ∠ 8 }
( ii ) Alternate Interior Angles.
As the name suggests these angles should be
Alternate and interior ( inside )
So the alternate interior angles are
( i ) ∠ 4 and ∠ 6 ( ii ) ∠ 3 and ∠ 5
( iii ) Alternate Exterior Angles.
As the name suggests these angles should be
Alternate and exterior ( outside)
So the alternate exterior angles are
( i ) ∠ 1 and ∠ 7 ( ii ) ∠ 2 and ∠ 8
( iv ) Interior Angles on the same side of the transversal.
As the name suggests these angles are ( i ) inside ( ii ) on the
left side and right side of the transversal.
So interior angles on the same side of the transversal are
( i ) ∠ 4 and ∠ 5 ( ii ) ∠ 3 and ∠ 6
Interior angles on the same side of the transversal are also called
consecutive angles, allied angles or co – interior angles.
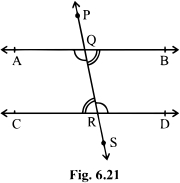
i ) If a ray stands on a line then the sum of two adjacent angles formed is 180°.
Eg. Ray OS stands of the line POQ
∴ ∠ POS + ∠ SOQ = 180°
ii ) If two lines intersect each other then the vertically opposite angles are equal
eg. Two lines AB and BC intersect at point O
∴ ∠ AOD = ∠ BOC and
∠ AOC = ∠ BOD
( ii ) If a transversal intersects two parallel lines then each pair
Of corresponding angles are equal
Eg. The corresponding angles are
a ) ∠ 1 and ∠ 5 b ) ∠ 2 and ∠ 6
c ) ∠ 3 and ∠ 7 d ) ∠ 4 and ∠ 8
( These same angles will be equal to each other if
The line ‘l’ and ‘m’are parallel )
If line l ∥ m then
∠ 1 = ∠ 5, ∠ 2 = ∠ 6, ∠ 3 = ∠ 7, ∠ 4 = ∠8

