7.2 CONGRUENCE OF TRIANGLES:
* If Δ PQR is congruent to Δ ABC we write Δ PQR ≅ Δ ABC.
Under a particular correspondence if Δ ABC ≅ Δ PQR, then it will not be correct to write
Δ BAC ≅ Δ PQR or ΔACB ≅ Δ PQR
* Two triangles are congruent if two sides and the included angle of one triangle is equal to the two sides and the included angle of the other triangle. (S.A.S. congruence rule)
* Two triangles are congruent if two angles and the included side of one triangle are equal to two angles and the included side of the other triangle (A.S.A. congruence rule)
* Two triangles are congruent if two pairs of angles and one pair of corresponding sides are equal. (A.A.S congruence rule)
Exercise 7.1
1. In quadrilateral ABCD, AC = AD and AB bisects ∠A .
(i) Show that Δ ABC ≅ Δ ABC. (ii) What can you say about BC and BD ?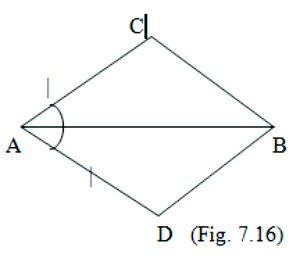
Given: AC =AD
To Prove: Δ ABC ≅ Δ ABD
Proof : In Δ ABC and Δ ABD
AC = AD and ∠CAB = ∠DAB (given )
AB = AB ( common side)
Using S.A .S congruence rule we get Δ ABC ≅ Δ ABD
BC= BD (c.p.c.t)
2. ABCD is a quadrilateral in which AD = BC and ∠DAB = ∠CBA . Prove that (i) Δ ABD ≅ Δ BAC (ii) BD = AC (iii) ∠ABD = ∠BAC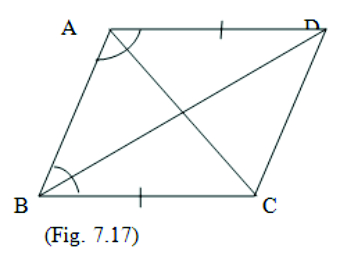 
Given: AD = BC and ∠DAB=∠CBA
To Prove: (i) ΔABD ≅ ΔBAC (ii) BD = AC (iii) ∠ABD = ∠B
Proof: (i) In ΔABD and ΔBAC we have AD = BC and ∠DAB = ∠DC
AB = BA (common side )
Using S.A.S congruence rule we get Δ ABD Δ BAC
(ii) Now since Δ ABD ≅ Δ BAC
and their corresponding parts are equal so we get BD = AC (c.p.c.t)
(iii) Since Δ ABD ≅ Δ BAC
and their corresponding parts are equal so we get ∠ABD = ∠BAC (c.p.c.t)
3. AD and BC are equal perpendiculars to a line segment AB . Show that CD bisects AB.
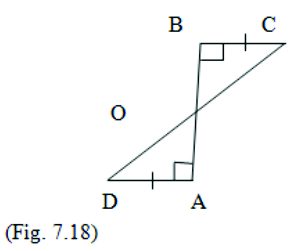Given : AD = BC and ∠DAO = ∠CBO = 90°
To Prove: OB = OA
Proof: In Δ OBC and Δ OAD we get
∠ABC = ∠BAD each side is 90°)
BC = AD (given )
∠BOC = ∠AOD (vertically opposite angles)
Using A.S.A congruence rule, we get Δ OBC ≅ Δ OAD
OB = OA (c.p.c.t) ( since O is the midpoint of AB )
So, CD bisects AB
4. l and m are two parallel lines intersected by another pair of parallel lines p and q (see Fig.7.19)
Show that Δ ABC ≅ Δ CDA.
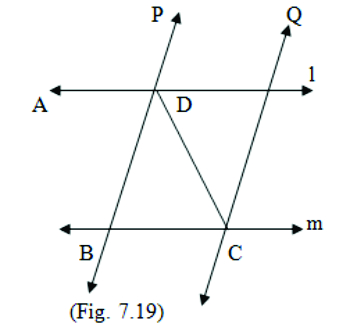Given: l ∥ m and p ∥ q
To prove: Δ ABC ≅ Δ CDA
Proof: Since l ∥ m and AC is the transversal
∠BAC = ∠DCA (alternate interior angles)
Δ ABC and Δ CDA we have ∠DCA and ∠BCA = ∠DAC ( proved )
AC = AC (common side)
Using A.S.A congruence rule we get Δ ABC ≅ Δ CDA
5. Line l is the bisector of an ∠A and B is any point on l. BP and BQ are perpendiculars from B to the arms of ∠A . Show that (i) Δ APB ≅ Δ AQB (ii) BP = BQ or B is equidistant from the arms of ∠A.
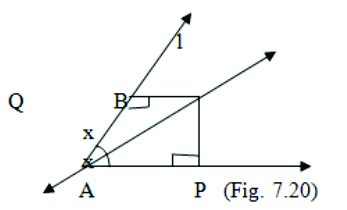
Given: line l is the bisector means ∠QAB = ∠PAB
BP and BQ are perpendiculars means ∠BQA = ∠BPA = 90°
To prove: (i) Δ APB ≅ Δ AQB (ii) BP = BQ
Proof: In Δ APB and Δ AQB we have AB = AB (common side)
∠PAB = ∠QAB (given)
∠ABP = ∠ABC (Third angle is equal if other two angles are equal)
By A.S.A congruence rule we get Δ APB ≅ Δ AQB
BP = BQ (c.p.c.t)
6. In the fig. AC = AE, AB = AD and ∠BAD = ∠EAC. Show that BC = DE.
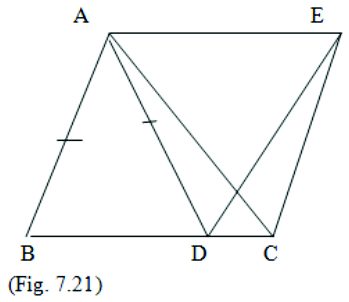
Given: AC = AE, AB = AD and ∠BAD = ∠EAC
To prove : BC = DE
Proof: We have (i) ∠BAD = ∠EAC (given)
Adding ∠DAC to both sides we get
∠BAD + ∠DAC = ∠EAC + ∠DAC ∠BAC = ∠DAE
Now in Δ ABC and Δ ADE we get ∠BAC = ∠DAE (proved)
AB = AD and AC = AE (given)
Δ ABC ≅ Δ ADE (S.A.S congruence rule)
(i ∴ BC = DE (c.p.c.t)
7. AB is a line segment and P is its mid-point. D and E are points on the same side of AB such that
∠BAD = ∠ABE and ∠EPA = ∠DPB. Show that (i) ΔDAP ≅ ΔEBP (ii) AD = BE
Given : P is the mid-point means AP = PB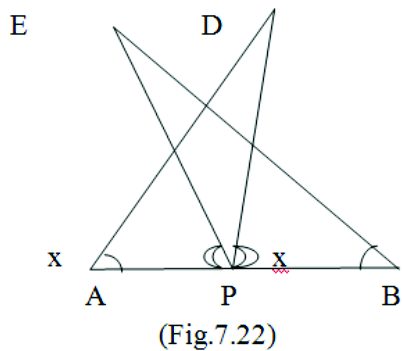 
∠BAD = ∠ABE and ∠EPA = ∠DPB
To prove:(i) Δ DAP ≅ ΔEBP (ii) AD = BE
Proof: (i) We have ∠EPA = ∠DPB (given)
Adding ∠EPD to both sides we get ∠EPA + ∠EPD = ∠DPB + ∠EPD ∠APD = ∠BPE
Now in Δ DAP and Δ EBP we have AP = PB (given)
∠PAD = ∠ PBE (since ∠A = ∠B) ∠DPA = ∠EPB (proved)
Using A.S.A congruence rule we get ΔDAP ≅ ΔEBP
(ii) Since ΔDAP ≅ ΔEBP we get AD = BE (c.p.c.t)
8.In right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see Fig.7.23). Show that: (i) ΔAMC ≅ ΔBMD
(ii) ∠DBC is a right angle (iii) ΔDBC ≅ ΔACB (iv) CM = AB
Given: ∠C = 900
DM = CM ( M is midpoint of AB ) AM = BM ( M is midpoint of AB )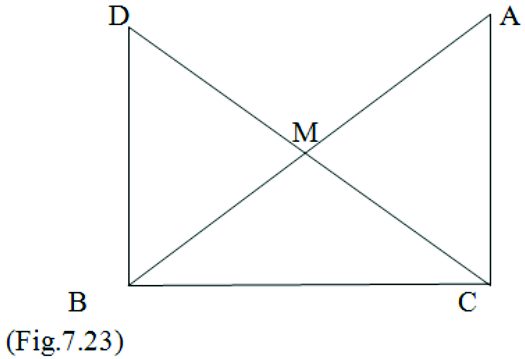 
To prove : (i) ΔAMC ≅ ΔBMD (ii) ∠DBC is a right angle (iii) ΔDBC ≅ ΔACB (iv) CM = AB
Proof: (i) In Δ AMC and ΔBMD we get
CM = DM and AM = BM (given)
∠AMC = ∠BMD (vertically opposite angles)
Using S.A.S congruence rule Δ AMC ≅ Δ BMD
(ii) Since Δ AMC ≅ Δ BMD ∠MAC = ∠MBD
These two angles are a pair of alternate interior angles and AC is parallel to DB
BC is the transversal that intersects parallel lines AC and DB
∠BCA + ∠DBC = 180° ⇒ 900 + ∠DBC = 1800
∠DBC = 1800 − 90 ⇒ ∠DBC = 900
(iii) Since Δ AMC ≅ Δ BMD
= BD (c.p.c.t)
DBC and Δ ACB we get ∠DBC = ∠ ABC (each angle = 900)
BD BD = CA (proved) BC = CB (common side)
Using S.A.S congruence rule Δ DBC ≅ Δ ACB
(iv) Since Δ DBC ≅ Δ ACB we get DC = AB (c.p.c.t)
But DM = CM and CM = DC = AB CM = AB