EXERCISE 3.5
1). Which of the following statements are true?
a) If a number is divisible by 3, it must be divisible by 9.
b) If a number is divisible by 9, it must be divisible by 3.
c) A number is divisible by 18 if it is divisible by both 3 and 6
d) If a number is divisible by 9 and 10 both, then it must be divisible by 90.
d) If two numbers are co-prime, at least one of them must be prime.
e) All numbers which are divisible by 4 must also be divisible by 8.
f) All numbers which are divisible by 8 must also be divisible by 4.
g) The sum two consecutive odd numbers is divisible by 4.
h) If a number exactly divides two numbers separately, it must exactly divide their sum.
i) If a number exactly divides the sum of two numbers. it must exactly divide the two numbers separately
Ans. a) false b) true c) false d) true e) false
f) false g) true h) true i) true j) false
2). Here are two different factor trees of 60. Write the missing number
a)
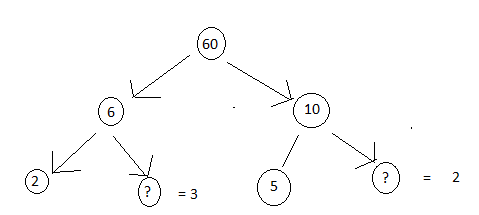
b)
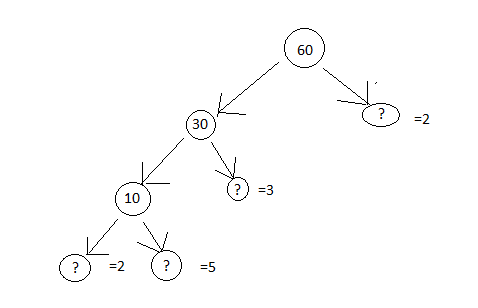
3). Which factors are not included in the prime factorisation of a composite number?
Ans. 1 and the number itself.
4). Write the greatest four digit number and express it in term of its prime factors.
Ans. The greatest four digit number is 9999. Its prime factor are = 3 x 3 x 11 x 101
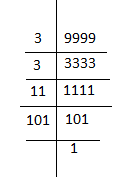
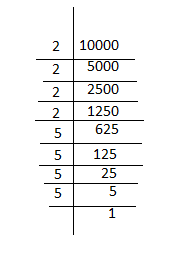
5). Write the smallest five digit number and express it in the form of its prime factor.
Ans. The smallest five digit number = 10000 Its prime factors are = 2 x 2 x 2 x 2 x 5 x 5 x 5 x 5
6). Find all the prime factors of 1729 and arrange them in ascending order. Now state the relation, if any; between two consecutive prime factors.
Ans. The prime factors of 1729 = 7 x 13 x 19. The difference between 2 consecutive
factors is 6
13 – 7 = 6
19 – 13 = 6
7). The product of three consecutive numbers is always divisible by 6. Explain this statement with help of some examples.
Ans. 2 x 3 x 4 = 24 which is divisible by 6. 7 x 8 x 9 = 504 which is divisible by 6.
8). In which of the following expression, prime factor has been done:
a) 24 = 2 x 3 x 4
Ans. Since 4 is composite, prime factorization has not been done.
b) 56 = 1 x 7 x 2 x 2 x 2
Ans. Since all the factors are prime, prime factorization has been done.
c) 70 = 2 x 5 x 7
Ans. Since all factors are prime, prime factorization has been done.
d) 54 = 2 x 3 x 9
Ans. Since 9 is a composite number, prime factorization has not been done.
9). Write the prime factorization of 15470
Ans. 15470 = 2 x 5 x 7 x 13 x 17

10). Determine if 25110 is divisible by 45.
Ans. 45 = 5 x 9
Factors of 5 = 1, 5
Factors of 9 = 1, 3, 9
Common factor = 1
∴5 and 9 are co- prime numbers.
The last digit of 25110 is 0, hence it is divisible by 5.
Sum of the digits 2 + 5 + 1 + 1 + 0 = 9
As 9 is divisible by 9 ∴ the number 25110 is divisible by 9.since the number is divisible by
both 5 and 9 ∴25110 is divisible by 45.
11). 18 is divisible by both 2 and 3. It is also divisible by 2 x 3 = 6. Similarly, a number is divisible by 4 and 6. Can we say that the number must be divisible by 4 x 6 = 24? If not, give an example to justify your answer.
Ans. No. number 12 is divisible by both 4 and 6 but 12 is not divisible by 24.
12). I am the smallest number, having four different prime factors. Can you find me?
Ans. Since it is the smallest number it will be the product of 4 smallest prime numbers 2 x 3 x 5 x 7 = 210

