7.4 MORE CRITERIA FOR CONGRUENCE OF TRIANGLES.
* If three sides of one triangle are equal to three sides of another triangle then the two triangles are congruent. This is S.S.S congruence rule.
* Two right angled triangles are congruent if one side and the hypotenuse of one triangle are respectively equal to the corresponding side and hypotenuse of the other triangle. This is R.H.S congruence rule.
Exercise 7.3
- Δ ABC and Δ DBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC . If AD is extended to intersect BC at P, show that : (i) Δ ABD ≅ Δ ACD (ii) Δ ABP ≅ Δ ACP (iii) AP bisects A as well as D (iv) AP is the perpendicular bisector of BC.Δ
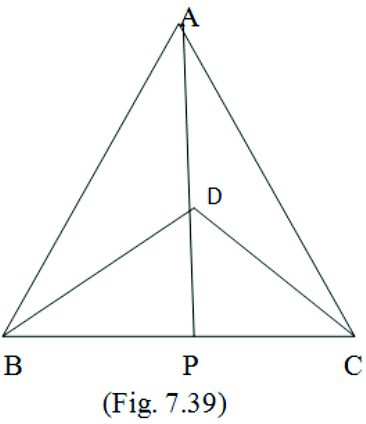
Given: AB = AC and BD = CD
To prove: (i) Δ ABD ≅ Δ ACD (ii) Δ ABP ≅ Δ ACP
(iii) AP bisects A as well as D (iv) AP is the perpendicular bisector of BC.
Proof: (i) In Δ ABD and Δ ACD we have AB = AC and BD = CD (given) AD = AD (common side) By S.S.S. congruence rule Δ ABD ≅ Δ ACD
(ii) In Δ ABP and Δ ACP we have AB = AC (given) ∠B =∠ C ( AB = AC, angles opposite to equal sides are equal ) AP = AP (common side) By S.A.S. congruence rule Δ ABP ≅ Δ ACP
(iii) Since Δ ABP ≅ Δ ACP Their corresponding parts are equal So, ΔBAP = ΔCAP (c.p.c.t) AP is bisector of ∠A ———– (1) In Δ BDP and Δ CDP we have BD = CD ( given ) ∠DBP = ∠CDP ( angles opposite to equal sides are equal ) DP = DP ( common side ) Δ BDP ≅ Δ CDP ∠BDP = ∠CDP AP is bisector of D ——— (2) From (1) and (2) AP is bisector of A and D (iv) We know that Δ ABP ≅ Δ ACP (proved) Δ APB = Δ APC (c.p.c.t) But ∠APB + ∠APC = 1800 (linear pair) ∠APB = ∠APC = 900 AP = BC AP is the perpendicular bisector of BC
2. AD is an altitude of an isosceles triangle ABC in which AB = AC. Show that (i) AD bisects BC (ii) AD bisects A.
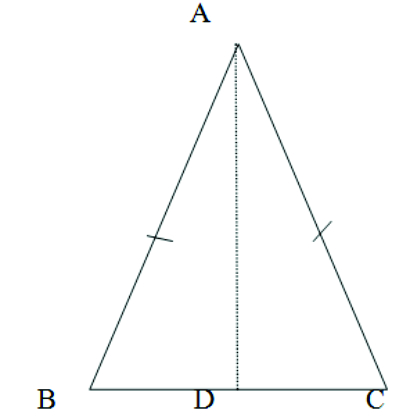
Given: AB = AC To prove: (i) AD bisects BC (to show BD = CD) (ii) AD bisects A ( to show ∠BAD = ∠CAD) Proof:(i) In Δ ABD and Δ ACD we have AB = AC (given) B = C (Angles opposite to equal sides are equal) AD = AD (common side) (side) By S.A.S congruence rule Δ ABD ≅ Δ ACD BD = CD (by c.p.c.t) It means D is the midpoint of BC (AD bisects BC ).
(ii) Since ∠ABD ≅ ∠ACD ∠BAD = ∠CAD ( by c.p.c.t) AD bisects ∠A
3.Two sides AB and BC and median AM of one triangle ABC are respectively equal to sides PQ and QR and median PN of Δ PQR. Show that : (i) Δ ABM ≅ Δ PQN, (ii) ΔABC ≅ ΔPQR
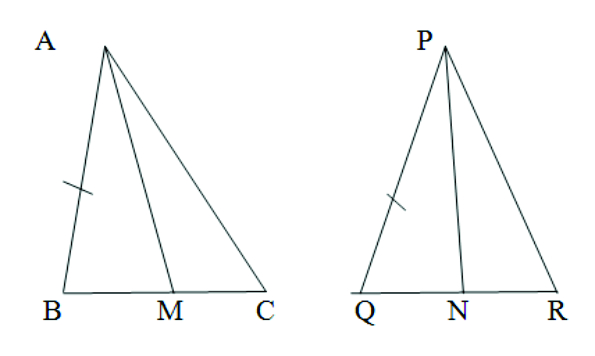
Given: AM and PN are medians, BC = QR, AB = PQ, PN = AM and QN = BM. To prove : (i) ΔABM ≅ ΔPQN, (ii) ΔABC ≅ ΔPQR Proof :(i) In ΔABC given that AM is a median BM = BC ————-(1) In ΔPQR PN is a median QN = QR ————-(2) But BC = QR (given) BM = QN (From (1) and (2)) In ΔABM and ΔPQN we have AP = PQ AM PN , AM = PN and BM = QN (given) By S.S.S congruence rule Δ ABM ≅ Δ PQN
(ii) Now Δ ABM ≅ Δ PQN (proved) ∠B = ∠Q (by c.p.c.t) Now in Δ ABC and Δ PQR we have ∠P = ∠Q (proved) AB = PQ , BC = QR (given ) By S.A.S congruence rule Δ ABC ≅ Δ PQR
4. BE and CF are two equal altitudes of a triangle ABC. Using RHS congruence rule, prove that the triangle ABC is isosceles. Given: BE = CF To prove: ΔABC is an isosceles triangle (to prove AB = AC ) Proof: We have BE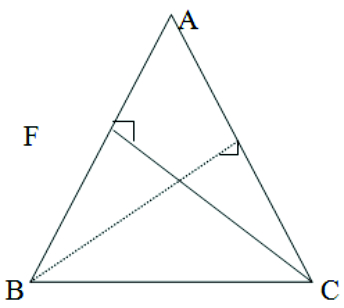
= AC ∠BEC = 90° and CF is perpendicular to AB. ∠CFB = 90° ( given )
In ΔBEC and ΔCFB (right angled ’s) BE = CF (given) BC = CB (common side) By R.H.S congruence rule BEC ≅ CFB So their corresponding parts are equal ∠BCE = ∠CBF or ∠BCA = ∠CBA AB = AC (sides opposite to equal angles of a triangle are equal) ABC is an isosceles triangle.
5. ABC is an isosceles triangle with AB =AC. Draw AP BC to show that B = C.
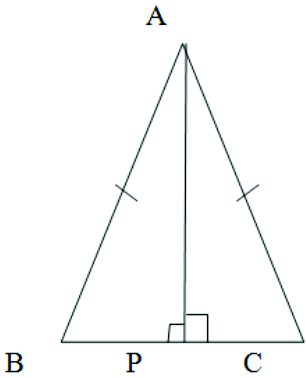Given: AB = AC Const: Draw AP perpendicular to BC To prove: ∠B = ∠C Proof: We have AP perpendicular to BC So ∠APB = 900 and ∠APC = 900 In Δ ABP and Δ ACP ( each = 900) AB = AC (given) AP = AP (common side) By R.H.S congruence rule Δ ABP ≅ Δ ACP ∠B = ∠C