7.5 SOME INEQUALITIES IN A TRIANGLE

7.5    SOME INEQUALITIES IN A TRIANGLE:

*  A triangle in which all three sides are different is called a scalene triangle.

Exercise 7.4

1. Show that in a right angled triangle, the hypotenuse is the longest side.

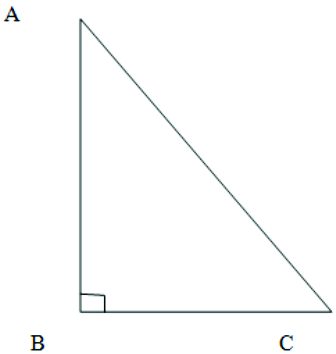
Given : ∠B = 90⁰

To Prove:  AC > BC and AC > AB

Proof:  In Δ ABC we get    ∠A + ∠B + ∠C = 180⁰ (angles of a triangle)               ∠A + 90⁰ + ∠C = 180⁰                ( B = 90⁰)                                                                          ∠A + ∠C =180°−  90°  =  90⁰                

i.e. ∠A + ∠C = B and so we get     B > C   and   B  > A                                               Side opposite to B is AC     and     Side opposite to C is AB                                   Side opposite to A is BC                                                                                                    ∴ ∴   AC > BC and AC > AB                                                                                                 AC is the longest side   and AC is also the hypotenuse                                                                                                                ∴ ∴   The hypotenuse is the longest side.

2. In Fig. 7.48, sides AB and AC of ABC are extended to points P and Q respectively. Also, PBC < QCB.                      Show that AC >AB.

Given:   ∠PBC < ∠QCB                                                                                                                                                                        To prove : AC > AB                                                                                                                                                                      Proof:   ∠PBC + ∠ABC = 180⁰ — (1)                                                                                                                                     ∠QCB + ∠ACB = 180⁰           —— (2) (both are linear pairs)                    From (1) and (2) we get    ∠PBC + ∠ABC = ∠QCB + ∠ACB                             But ∠PBC  <  ∠QCB (given)                                                                      ∠ABC  >  ∠ACB                                                                                                  Side opposite to ABC  is  AC                                                                                  Side opposite to ACB  is  AB                                                                                  AC  >  AB

3. In Fig. 7.49, B < A and C < D. Show that AD<BC.

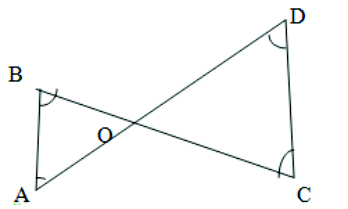
Given: B < A and C  To prove:  AD < BCProof: B < A (given)  ∴  A > B

Side opposite A is OB                           Side opposite B is OA                                 AB >OA  ——–(1)    In the same way OC  > OD  ———–(2)                                                                                                                                  From (1) and (2) we get                                                                                                                                                                 [OB+ OC ]  >  [OA + OD]                                                                                                                                                                 BC > AD                                                                                                                                                                                                     i.e.  AD < BC

4. AB and CD are respectively the smallest and longest sides of a quadrilateral ABCD (see Fig. 7.50). Show that A > C and B> D.

 

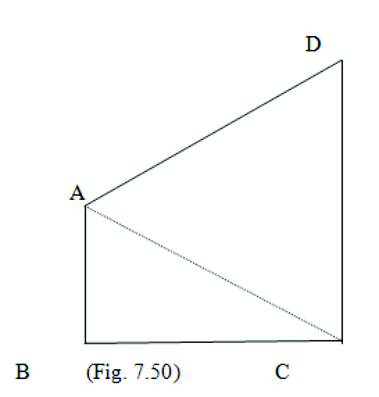Solution:

Given: AB is smallest side

And  CD is longest side

To prove:  A > C and B > D

Const: Join AC

Proof: In ABC we get

BC > AB ( AB is smallest side)

Angle opposite to BC is BAC

Angle opposite to AB is BCA

BAC> BCA  —————–(1)

In ACD we get

CD > AD (CD is the longest side)

Angle opposite to CD is CAD

Angle opposite to AD is ACD

CAD  > ACD  —————–(2)

Adding (1) and (2) we get

BAC + CAD = BCA + ACD

A > C

By joining BD we will get B > D

 

5. In Fig.7.51, PR >PQ and PS bisects QPR. Prove that PSR > PSQ.

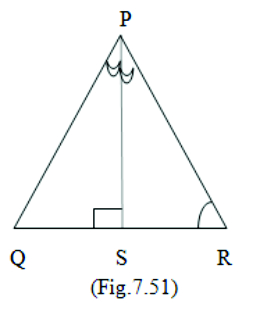
Solution:

Given:   PR > PQ and PS bisects QPR means QPS = RPS

To prove: PSR > PSQ

 Proof:

QPS = RPS (PS bisects QPR)  (given) ——(1)

PR > PQ (given)

Angle opposite to PR is PQS

Angle opposite to PQ is PRS

PQS > PRS         —————— (2)

Adding (1) and (2) we get

( PQS + QPS) > ( PRS + RPS)

We know that in triangles the exterior angle is equal to

the sum of the interior opposite angles)

PSR = PQS + QPS

And PSQ = PRS + RPS

From above we get

PSR > PSQ

 

6. Show that of all line segments drawn from a given point not on it, the perpendicular line segment in the shortest.

Solution:

Given: PQ, PR and PS are line segments

To prove: PQ is the shortest line segment

Proof: PQ is the perpendicular on line QS and

PR and PS are any other two line segments

We know that in a triangle if one angle is 90⁰

Then the other angles have to be lesser than 90⁰

Here for perpendicular PQ we get

PQR > PRQ (for  PQR)

Also PQR > PSQ (for  PSR)

PR > PQ and PS > PQ

PQ is the shortest line segment

The perpendicular line segment is the shortest