8.2 PROPERTIES OF QUADRILATERALS:
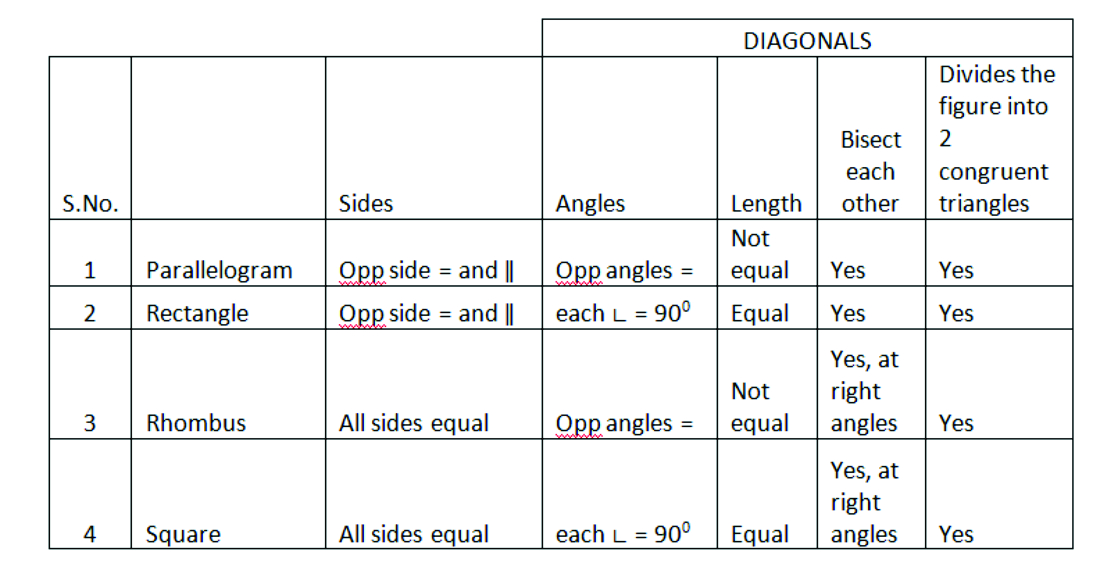
- Properties of parallelograms:
- Opposite sides are equal and parallel
- Opposite angles are equal
- Diagonals bisect each other
- Each diagonal divides the parallelograms into two congruent triangles.
- Properties of Rectangle:
- Opposite sides are equal and parallel.
- Each angle is 900
- Diagonals are of equal length and bisect each other.
- Each diagonal divides the rectangle into two congruent triangle
- Properties of Rhombus:
- All sides are of equal length.
- Opposite angle are equal.
- Diagonals bisect each other at right angles.
- Each diagonal divides the rhombus into two congruent triangles.
- Properties of Square:
- All sides are of equal length.
- Each angle is 900
- Diagonals are of equal length and bisect each other at right angles.
- Each diagonal divides the square into two congruent triangles.
Exercise 8.1
- The angles of quadrilateral are in the ration 3 : 5 : 9 : 13. Find all the angles of the quadrilateral.
Solution: Let the multiplicative value of the ratio be x.
The ratio 3 : 5 : 9 : 13 becomes 3 x, 5 x, 9 x, 13 x.
Sum of all the angles of a quad is 3600
3 x + 5 x + 9 x + 13 x = 3600
30 x = 360° ⇒ x = 120
∴ The first angle is 3 x = 3 x 12 = 360
∴ The second angle is 5 x = 5 x 12 = 600
∴ The third angle is 9 x = 9 x 12 = 1080
∴ The second angle is 13 x = 13 x 12 = 1560
∴ The four angles are 360, 600, 1080, 1560
2. If the diagonals of a parallelogram are equal, then show that it is a rectangle.
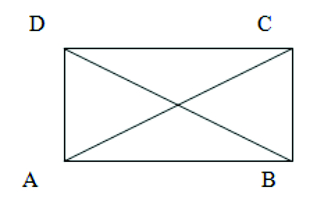
Given : AC = BD
To prove: ABCD is a rectangle
Proof: In Δ DAB and Δ CBA
AD = BC (opposite sides of a parallelogram)
AC = BD (given)
By S.S.S congruence rule
Δ DAB ≅ Δ CBA
∠DAB = ∠CBA (c.p.c.t) ————– (1)
Since ABCD is a parallelogram
AD is parallel to BC and AB is the transversal .
∠DAB + ∠CBA = 1800 (sum of interior angles on same side of transversal is 1800) ———– (2)
From (1) and (2) we get
∠DAB = 900 and ∠ CBA = 900
Hence the parallelogram is a rectangle.
3.Show that if the diagonals of a quadrilateral bisect each other at right angles, then it is a rhombus.
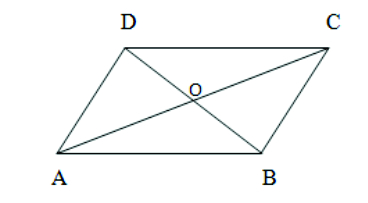
Given: ∠AOB = ∠BOC = ∠COD = ∠DOA = 900
To prove : AB = BC = CD = DA
Proof: In Δ AOB and Δ AOD, we have
AD = AD ( common side )
OB = OD (O is midpoint of BD)
Δ AOB = Δ AOD (given)
By S.A.S. congruence rule
Δ AOB ≅ Δ AOD So their corresponding parts are equal
AD = AB, AB = BC, BC = CD, CD = AD
So we have AB = BC = CD = DA
Thus the quadrilateral ABCD is a rhombus.
4. Show that the diagonals of a square are equal and bisect each other at right angles.
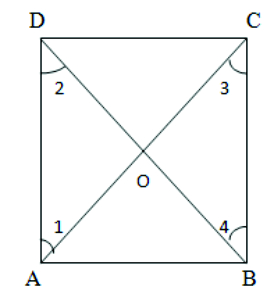
Given: AB = BC = CD = DA (all sides of a square are equal)
A = B = C = D = 900 (angles of a square)
To prove: (i) AC = BD
(ii) OA = OC and OB = OD
(iii) ∠AOB = ∠BOC = ∠COD = ∠AOD = 900
Proof: In Δ ABC and Δ BAD we have
AB = AB (common side)
BC = AD (opposite sides of square)
∠ABC = ∠BAD (each = 900)
By S.A.S congruence rule we get Δ ABC ≅ Δ BAD
∴ AC = BD (c.p.c.t)
(ii) AD is parallel to BC and AC is the transversal.
∠1 = ∠3 and ∠2 = ∠4 (interior alternate angles)
In Δ OAD and Δ OCB we have
AD = BC (opposite sides of a square)
∠1 = ∠3 and ∠2 = ∠4 ( both are proved )
Δ OAD ≅ Δ OCB
( By A.S.A congruence rule )
OA = OC and OD = OB ( both are c.p.c.t.)
(iii) In ΔOBA and ΔODA we have
AB = AD (opposite sides of a square)
OB = OD (proved)
OA = OA (common side)
By S.S.S congruence rule we get ,
ΔOBA ≅ ΔODA
∠AOB = ∠AOD (c.p.c.t)
But ∠AOB + ∠AOD = 1800 (linear pair)
∠AOB = ∠ AOD = 90° ⇒ AC = BD
From above we get AC and BD are equal and bisect each other at right angles.
5. Show that if the diagonals of a quadrilateral are equal and bisect each other at right angles, then it is a square.
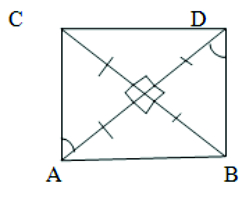
Given: AC = BD and ∠AOB = ∠BOC = ∠COD = ∠AOD = 900
To prove: (i) AD = BC = AB = DC and AB = BC = CA = AD
(ii) ∠DAB = ∠ABC = ∠BCD = ∠CDA = 900
Proof: In Δ AOD and Δ AOB we have
AO = AO (common side)
OD = OB (O is the mid point of AB)
∠AOD = ∠AOB (each angle is 90)
By S.A.S. congruence rule we have
Δ AOD ≅ Δ AOB ∴ Their corresponding parts are equal
AD = AB, AB = BC, BC = CD, CD = DA
AB = BC = CA = DA ———-(1) (All four sides are equal)
In ΔAOD and ΔCOB we have
AO = CO and OD = OB ( both are given )
∠AOD = ∠COB (each is 900 ) and so we get Δ AOD ≅ Δ COB
But they are a pair of interior alternate angles
AD = BC ————(2)
Similarly we can show AB = DC ———- (3)
From (1), (2) and (3) we can say that
All four sides are equal and opposite sides are also parallel to each other
(ii) In Δ ABC and Δ BAD we have AC = BD (given)
BC = AD (proved) and AB = BA (common side)
By S.S.S congruence rule we get ∠ABC = ∠BAD
Since AD is parallel to BC and AB is a transversal
∠ABC + ∠BAD = 1800 interior opposite angles = 180° )
Since ∠ ABC = ∠BAD we get Δ ABC ≅ Δ BAD (c.p.c.t)
∠ABC = ∠BAD = 90° and similarly we get ∠ADC = ∠BCD = 900
6. Diagonal AC of a parallelogram ABCD bisects ∠A (see fig.8.19). Show that (i) it bisects ∠C also. (ii) ABCD is a rhombus.
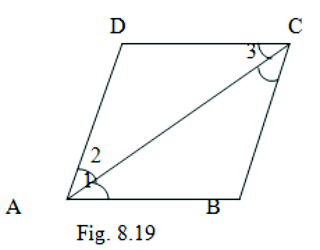
Given: ∠DAC = ∠BAC ( AC bisects ∠A )
To prove: (i) ∠DCA = ∠BCA (AC bisects ∠C ) (ii) ABCD is a rhombus
Proof: Since ABCD is a parallelogram
(i) AB is parallel to DC and AC is the transversal
∠ 1 = ∠3 (interior alternate angles) ——- (1)
Also BC is parallel to DA and AC is the transversal
∠2 = ∠4 (interior alternate angles) —— (2)
But it is given that ∠DAC = ∠BAC ⇒ ∠1 = ∠2 ——- (3)
From (1), (2) and (3) we get ∠3 = ∠4
∠DCA = ∠BCA ( AC bisects ∠C )
(ii) In ABC we get ∠1 = ∠4 ( proved )
BC = AB ( sides opposite to equal angles ) ——- (4)
∠2 = ∠3 (proved)
AD = DC ( sides opposite to equal angles ) —— (5)
But we are given that ABCD is a parallelogram
And so AB = DC ———– (6)
From (4), (5) and (6) we get
AB = BC = CD = DA ∴ ABCD is a rhombus.
7. ABCD is a rhombus. Show that diagonal AC bisects A as well as C and diagonal BD bisects B as well as D.
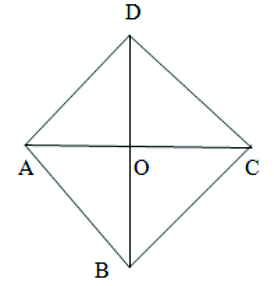
Given: ABCD is a rhombus.
To prove: (i) AC bisects A and C and (ii) BD bisects B and D.
Proof: In Δ ADC and Δ ABC
AD = AB (sides of a rhombus)
CD = CB (sides of a rhombus)
AC = AC (common side)
By S.S.S. congruence test we get ∆ ADC ≅ ∆ ABC.
Their corresponding parts are equal.
∠DAC = ∠BAC and ∠DCA = ∠BCA (c.p.c.t)
Hence AC bisects the two angles ∴ ∠ A = ∠C.
Similarly take Δ BAD and Δ BCD and show that BD bisects the two angles ∴ ∠B = ∠D.
8. ABCD is a rectangle in which diagonal AC bisects ∠A as well as ∠C. Show that (i) ABCD is a square (ii) diagonal BD bisects B as well as D.
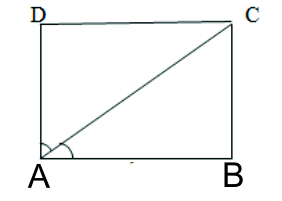
Given: (i) ABCD is a rectangle and (ii) AC bisects ∠A and ∠C
To prove: (i) ABCD is a square and (ii) Diagonal BD bisects B and D
Proof: In Δ ADC and Δ ABC we have
∠DAC = ∠BAC ( AC is bisector of ∠A )
∠DCA = ∠BCA ( AC is the bisector of ∠C )
AC = AC ( common side )
∆ ADC ≅ ∆ ABC ( By A.S.A congruence rule. )
Their corresponding parts are equal and so we get AD = AB (c.p.c.t)
So in rectangle ABCD if adjacent sides are equal then we can say that ABCD is a square.
(ii) In ΔDAB and ΔBCD we have
AD = BC and CD = DA (both are opposite sides of a square)
BD = BD (common side)
By S.S.S. congruence test, we get ∆ DAB ≅ ∆ DCB
Now we get ∠ADB = ∠ CDB and ∠ABD = ∠CBD
( both the corresponding parts are equal of the above two triangles )
So we can say that ∆ ADC ≅ ∆ ABC
BD bisects both ∠B and ∠D and so we get ∠B = ∠D
9. In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP = BQ (see Fig.8.20). Show that (i) ΔAPD ≅ ΔCQB (ii) AP = CQ (iii) ΔAQB ≅ ΔCPD (iv) AQ = CP (v) APCQ is a parallelogram.
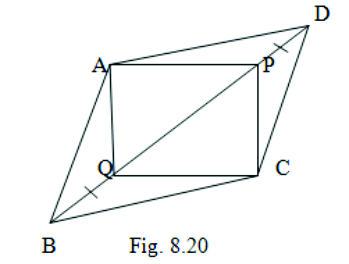
Given: DP = BQ
To prove: (i) ∆ APD ≅ ∆ CQB (ii) AP = CQ (iii) ∆ AQB ≅ ∆ CPD (iv) AQ = CP (v) APCQ is a parallelogram.
Proof: Consider ∆ APD and ∆ CQB
Since ABCD is a parallelogram and AD ∥ BC
and BD is the transversal we get
∠CBQ = ∠ADP (interior alternate angles)
AD = CB (opposite sides of a parallelogram)
PD = QB (given)
By S.A.S congruence rule we get
∆ APD ≅ ∆CQB
(ii) ∆ APD ≅ ∆CQB ( proved) Their Their corresponding parts are equal and
∴ AP = CQ (c.p.c.t)
(iii) In ∆ AQB and ∆CPD
Since ABCD is a parallelogram and AB ∥ CD and BD is the transversal
∠ABQ = ∠CDP ( alternate interior angles )
QB = PD ( given ) and AB = CD ( opposite sides of parallelogram )
By S.A.S congruence rule we get ∆ AQB ≅ ∆ CPD
(iv) ∆ AQB ≅ ∆CPD ( proved )
Their corresponding parts are equal
∴ AQ = CP (c.p.c.t).
(v) Join AC. Now, since the diagonals of a parallelogram bisect each other we get
AO = CO ————(1)
And BO = DO (diagonals of a parallelogram bisect each other)
∴ QO = OP ( BQ = DP is given) ————- (2)
From (1) and (2) we get
AO = CO and QO = PO
AC and QP bisect each other at O
∴ APCQ is a parallelogram.
10. ABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD (see Fig.8.21). Show that (i) ΔAPB ≅ Δ CQD (ii) AP = CQ
Given: (i) BD is a diagonal (ii) ABCD is a parallelogram
(iii) AP ⊥ BD and CQ ⊥ BD
To prove: (i) ∆ APB ≅ ∆CQD (ii) AP = CQ
Proof: In ∆ APB and ∆ CQD we have
∠APB = ∠CQD ( both are 90° each )
AB = CD (opposite sides of a parallelogram)
∠APB = ∠CQD (AB ∥ CD and AB is transversal so interior angles are equal)
By A.A.S congruence rule we get
∆ APB ≅ ∆ CQD
(ii) Since ∆ APB ≅ ∆ CQD their corresponding parts are equal
∴ AP = CQ (c.p.c.t)
11. In ABC and DEF, AB = DE, AB DE, BC = EF and BC is parallel to EF. Vertices A, B and C are joined to vertices D, E and F respectively.
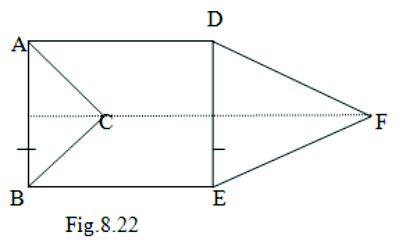Show that (i) quadrilateral ABCD is a parallelogram. (ii) quadrilateral BEFC is a parallelogram (iii) AD is parallel to CF an d AD = CF (iv) quadrilateral ACFD is a parallelogram (v) AC = DF and (vi) ΔABC ≅ ΔDEF
Given: (i) AB = DE (ii) BC = EF and (iii) BC ∥ EF To prove: (i) quadrilateral ABED is a parallelogram
(ii) quadrilateral BEFC is a parallelogram
(iii) AD ∥ CF and AD = CF
(iv) quadrilateral ACFD is a parallelogram
(v) AC = DF (vi) ∆ ABC ≅ ∆ DEF
Proof: AB = DE (given) and AB ∥ DE (given)
A quadrilateral in which a pair of opposite sides is equal and parallel then it is a parallelogram
∴ ABED is a parallelogram
(ii) BC = EF (given) and BC ∥ EF (given)
A quadrilateral in which a pair of opposite sides is equal and parallel then it is a parallelogram
∴BECF is a parallelogram
(iii) Since ABED is a parallelogram (proved)
AD ∥ DE and AD = BE ———–(1)
Again since BEFC is a parallelogram (proved)
BE ∥ CF and BE = CF ———–(2)
(opposite sides are equal and parallel in (1) and (2) )
From (1) and (2) we get AD ∥ CF and AD = CF
(iv) AD ∥ CF and AD = CF
A quadrilateral in which a pair of opposite sides is equal and parallel then it is a
parallelogram ∴ ACFD is a parallelogram
(v) Since ACFD is a parallelogram (proved)
Its opposite sides are parallel and equal
∴ AC = DF
(vi) In ∆ ABC and ∆DEF we have
AB = DE (given) and BC = EF (proved) and AC = DF (proved)
By S.S.S congruence rule we get
∆ ABC ≅ ∆ DEF
12. ABCD is a trapezium in which AB ∥ CD and AD = BC (see Fig.8.23). Show that (i) ∠A = ∠B (ii) ∠C = ∠D (iii) ∆ ABC ≅ ∆BAD (iv) diagonal AC = diagonal BD (Hint : Extend AB and draw a line through C parallel to DA intersecting AB produced at E )
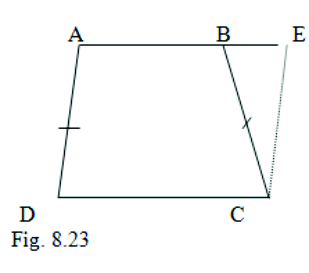
Given: ( i ) AB ∥ CD and (ii) AD = BC
To prove: (i) ∠A = ∠B (ii) ∠C = ∠D
(iii) ∆ ABC ≅ ∆ BAD (iv) diagonal AC = diagonal BD
Const: Extend AB and draw a line through C parallel to DA intersecting AB produced to E
Proof: (i) AB ∥ CD and AD = BC ( given )
and AD ∥ CE and AE ∥ DC ( by construction )
∴ AECD is a parallelogram
AD = CE ( opposite sides of parallelogram AECD )
AD = BC (given)
∴ We get BC = CE
∴ ∠CBE = ∠CEB (angles opposite to equal sides are equal) —- (1)
∴ ∠ABC + ∠CBE = 180° ( linear pair ) ———– (2)
∠CEB + ∠A = 180° (adjacent angles of a parallelogram = 180° ) —– (3)
From (2) and (3) we get
∠ABC + ∠CBE = ∠CEB + ∠A
∴ ∠ABC = ∠A ( since ∠CBE = ∠CEB ( proved )
∴ ∠B =∠A ∴ ∠A =∠B
(ii) AB ∥ CD and AD is transversal
∴ ∠A +∠D = 180° (interior opposite angles sum is 180°)
Similarly ∠B +∠C = 180° (interior opposite angles sum is 180°)
∴ ∠A + ∠D = ∠B + ∠C
∠D = ∠C ( since ∠A = ∠B already proved ))
∴ ∠C = ∠D
(iii) In ∆ ABC and ∆BAD we get
AB = BA (common side )
BC = AD ( given )
∠ABC = ∠A = ∠BAD (proved)
∴ ∆ ABC ≅ ∆BAD ( By S.A.S congruence rule )
(iv) We know that ∆ ABC ≅ ∆BAD
Their corresponding parts are equal
∴ AC = BD ( diagonals ) (c.p.c.t)