8.3 THE MID POINT THEOREM:
The midpoint theorem states that the line segment joining the line segment joining the mid points of two sides of a triangle is parallel to the third side.
The line drawn through the mid point of one side of a triangle parallel to another side bisects the third side.
Exercise 8.2
1. ABCD is a quadrilateral in which P,Q, R and S are mid-point of the sides AB, BC, CD and DA and AC is a diagonal. Show that : (i) SR ∥ AC and SR = 1/2 AC (ii) PQ = SR (iii) PQRS is a parallelogram.
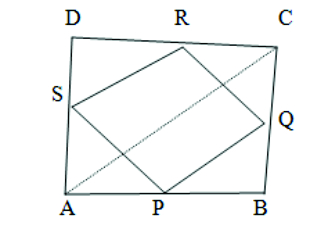Given: (i) RC = RD (ii) SD = AS
(iii) AP = PB (iv) QC = QB
To prove: (i) SR ∥ AC and SR = 1/2 AC
(ii) PQ = SR (iii) PQRS is a parallelogram
Proof: (i) In ∆ ACD we have S and R as the mid-point of sides AD and DC respectively.
We know that a line segment joining the mid-points of two sides of a triangle is parallel to the third side and is half of it.
∴ SR ∥ AC and SR = 1/2 AC
(ii) From (i) we get SR ∥ AC and SR = 1/2 AC ——— (1)
Consider ∆ ABC we have P and Q as mid-points of sides AB and BC respectively.
∴ PQ ∥ AC and PQ = 1/2 AC (mid-point theorem) ————(2)
From (1) and (2) we get
SR ∥ PQ and SR = PQ
∴ SR = PQ
(iii) Now SR = PQ (proved)
And SR ∥ PQ
∴ PQRS is a parallelogram
2. ABCD is a rhombus and P, Q, R and S are the midpoints AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rectangle.
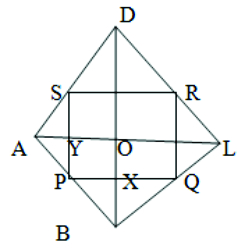Given: ABCD is a rhombus
P, Q, R and S are the midpoints AB, BC, CD and DA respectively
To prove: PQRS is a rectangle
Proof: First we have to prove that PQRS is a parallelogram
and then we have to prove that PQRS is a rectangle
(i) Consider ∆ ACD,
S and R are the mid-points of sides AD and DC respectively
(By mid-point theorem statement)
SR ∥ AC and SR = 1/2 AC ————-(1)
Consider ∆ABC,
P and Q are the mid-points of sides AB and BC respectively
(By mid-point theorem statement)
PQ ∥ AC and PQ = 1/2 AC ———–(2)
From (1) and (2) we get
SR ∥ AC and PQ ∥ AC → SR ∥PQ – ———-(3)
And SR = 1/2 AC and PQ = 1/2AC → SR = PQ ———(4)
From (3) and (4) we get PQRS is a parallelogram
(ii) As PX ∥ YO and PY ∥ OX
We get PXOY is a parallelogram
Since ABCD is a rhombus we know that diagonals of a rhombus (AC and BD) bisect each other and are at right angles ∴ ∠AOB = ∠YOX = 90°
But ∠YOX = ∠YPX = 90° (opposite angles of a parallelogram)
∴ ∠YPX = ∠SPQ = 90°
∴ PQRS is a rectangle.
3. ABCD is a rectangle and P, Q, R and S are the midpoints AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.
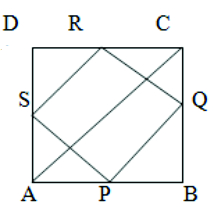Given: ABCD is a rectangle
P, Q, R and S are the midpoints AB, BC, CD and DA
To prove : The quadrilateral. PQRS is a rhombus
Const: Join AC
Proof: We have to first prove that PQRS is a parallelogram and
then we can prove that PQRS is a rhombus
(i) In ∆ ABC we have
PQ = 1/2 AC and PQ ∥ AC —-(1) (mid-point theorem)
In ∆ ACD we have,
SR = 1/2 AC and SR ∥ AC —-(2) (mid-point theorem)
From (1) and (2) we get,
PQ ∥ AC and SR ∥ AC gives us PQ ∥ SR
PQ = 1/2 AC and SR = 1/2 AC gives us PQ = SR
∴ We get PQ = SR and PQ ∥ SR ——— (3)
Similarly by joining BD we will get
PS = QR and PS ∥ QR ——– (4)
From (3) and (4) we get both pairs of opposite sides of quad. PQRS are equal and parallel.
∴ PQRS is a parallelogram
(ii) Now in ∆PAS and ∆PBQ
∠A = ∠B ( each angle is 90° )
AP = PB ( P is mid point of AB )
AS = BQ (∵ 1/2 AD = 1/2 BC )
By S.A.S. congruence rule we get
∆PAS ≅ ∆PBQ ∴ Their corresponding parts are equal
PS = PQ (c.p.c.t)
PS = QR and PQ = SR (proved)
PS = PQ = QR = SR
All sides are equal
∴ PQRS is a rhombus
4. ABCD is a trapezium in which AB ∥ DC, BD is a diagonal and E is the mid-point of AD. A line is drawn through E parallel to AB intersecting BC at F . Show that F is the mid-point of BC.
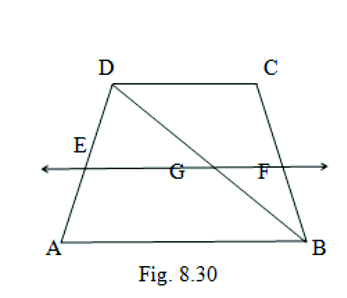
Given: AB ∥ DC, BD is a diagonal ,
E is the mid-point of AD.
To prove: CF = BF
Proof: E is the mid-point of AD (given)
and EG ∥ AB
Using the converse of mid-point theorem
we get G is the mid point of BD
In ∆BDC
G is the mid-point of BD
GF ∥ DC
Using the converse of mid-point theorem we get F is the mid point of BC.
5. In a parallelogram ABCD, E and F are the mid-points of sides AB and CD respectively . Show that the line segments AF and EC trisect the diagonal BD.
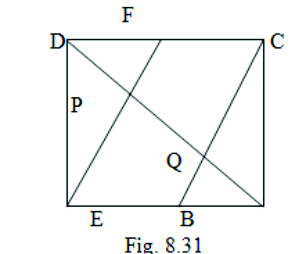Given: E is the mid-point of AB and F is the mid-point of CD
To prove: DP = PQ = QB
Proof: AB = CD (opposite sides of a parallelogram)
∴ 1/2 AB = 1/2 CD
∴ AE = CF —— (1) ( E and F are mid-points)
Now AB ∥ CD
∴ 1/2 AB ∥ 1/2 CD
∴ AE ∥ CF ——(2) ( E and F are mid-points)
From (1) and (2) we get AECF is a parallelogram
In ∆ DBC
F is the mid-point of DC (given)
and FP ∥ CQ (∵ AF ∥ CE)
P is the midpoint of DQ (by converse of mid-point theorem)
∴ DP = PQ – ——–(3)
Similarly in ∆ BAP
BQ = PQ ———-(4)
From (3) and (4) we get
DP = PQ = BQ
∴ The line segments AF and EC trisect the diagonal BD.
6. Show that the line segments joining the mid-points of the opposite sides of a quadrilateral bisect each other.
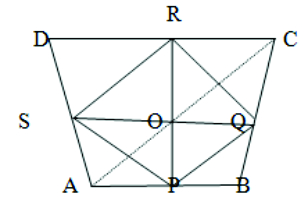Given: P,Q,R,A are the mid-points of AB, BC, CD and DA
To prove: The line segments bisect each other
Proof: Join PQ, QR, RS and SP
Also join PR and SQ
In ∆ ABC we have P and Q as mid-points
of sides AB and AC respectively
∴ PQ ∥ AC and PQ = 1/2 AC ——(1)
Similarly in ∆ ADC
RS ∥ AC and RS = 1/2 AC ——–(2)
From (1) and (2) we get
PQ ∥ RS and PQ = RS
∴ PQRS is a quadrilateral. And a pair of opposite sides (PQ and RS) are equal and parallel
∴ PQRS is a parallelogram
We know that the diagonals of a parallelogram bisect each other
Here PR and SQ bisect each other
So, the line segments joining the mid-points of the opposite sides of a quadrilateral. ABCD bisect each other
7. ABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that (i) D is the mid-point of AC (ii) MD ⊥ AC (iii) CM = MA = 1⁄/2 AB.
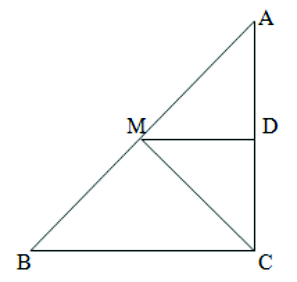Given: (i) ∠C = 90° (ii) AM = BM and MD ∥ BC
To prove: (i) D is the mid-point of AC
(ii) MD ⊥ AC
(iii) CM = MA = 1/2 AB.
Proof: In ∆ ACB we have
(i) M is mid-point of AB and MD ∥ BC (both are given)
Using the converse of mid-point theorem we get
D is the mid-point of AC
(ii) Since MD ∥ BC (given) and AC is the transversal
∠MDA = ∠BCA (corresponding angles)
∴∠MDA = ∠BCA = 90° (given ∠BCA = 90°)
∴ MD ⊥ AC
(iii) In ∆ ADM and ∆ CDM we have
∠ADM = ∠CDM (each angle is 90°)
MD = MD (common side)
AD = CD (D is mid-point of AC)
By S.A.S congruence rule we get ∆ ADM ≅ ∆ CDM
∴ MA = MC ( c.p.c.t ) ———- (1)
M is mid-point of AC
∴ AM = 1/2 AB ———–(2)
From (1) and (2) we get
CM = MA = 1/2 AB