8.4 ADDITIONAL QUESTIONS AND ANSWERS

8.4  ADDITIONAL QUESTIONS AND ANSWERS;

1. The sum of the angles of a quadrilateral is 360⁰.

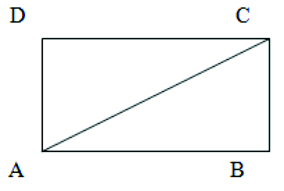
Given :  ABCD is a quadrilateral

To prove: A + B + C + D = 360⁰

Construction : Join AC

Proof:  Consider ADC

∴   ∠ ADC + ∠ DCA +∠ CAD = 180⁰      ———-(1)

(sum of the angles of a triangle is  180⁰ )

Consider Δ ABC

∴  ∠ ABC + ∠ BCA + ∠ CAB = 180⁰        ———-(2)

(sum of the angles of a triangle in 180⁰)

Adding (1) and (2) we get

∠ ADC + ∠ DCA + ∠ CAD + ∠ ABC + ∠ BCA + ∠ CAB = 180⁰ + 180⁰

(Arranging in order we get)

∠ ADC + ( ∠ DCA + ∠ BCA) + (  ∠ CAD + ∠ CAB ) + ∠ ABC  = 360⁰

(Now ∠ DCA +∠ BCA = C    and  ∠ CAD + ∠ CAB = A)

∠ ADC + ∠ C  + ∠ A +∠ ABC  = 360°        ⇒        ∠ D + ∠ C  + ∠ A + ∠B  = 360⁰

∠ A + ∠ B  + ∠ C + ∠ D  = 360⁰        proved

2. If each pair of opposite sides of a quadrilateral is equal then it is a parallelogram.

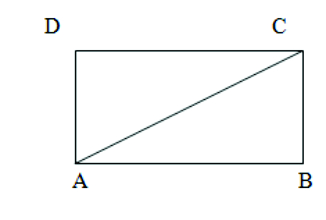
Given : (i)  AB = CD     (ii)  AD = BC

To prove : ABCD is a parallelogram

Construction : Join AC

Proof:  Consider ABC  and  CDA

AB = DC         and   AD = BC         (given)

AC = AC        (common side)

ABC  ≅ CDA     (By SSS test)

So ∠BAC  = ∠DCA        and     ∠BCA  =  ∠DAC            (c.p.c.t)

If ∠BAC  =  ∠DCA  then as they are interior opposite angles we get AB is parallel to  CD

If ∠BCA  = ∠DAC  then as they are interior opposite angles we get AD is parallel to  BC

Since opposite sides are equal and parallel we get   ABCD is a parallelogram.

3.  Diagonal PR of a parallelogram PQRS bisects P.   Show that   (i) it bisects R also,      (ii)  PQRS is a rhombus.

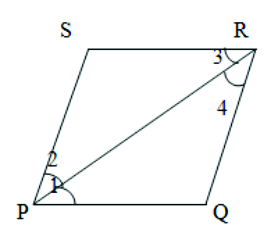
Given:  SPR  =  QPR               (PR bisects P)

To prove:  (i)  SRP  =  QRP    (PR bisects R)    (ii)  PQRS  is  a  rhombus

Proof:  Since PQRS  is  a parallelogram

(i)  PQ = RS   and PR is a transversal

∠ 1  = ∠ 3          (interior alternate angles)   ——-  (1)

Also PQ = QR   and PR is a transversal

∠2  =  ∠4           (interior alternate angles)   ——- (2)

But we know that    ∠ SPR  =  ∠ QPR                        (given)      ———– (3)

From  (1),  (2)  and  (3)  we  get

∠ 3 = ∠ 4    ⇒        PR bisects R

∠ SRP   =  ∠ QRP

(ii)  In   Δ PQR  we  get

∠1 = ∠4             (since ∠ 1  = ∠ 2 = ∠ 4)       ———-        (4)

QR = PQ   (sides opposite to equal angles are equal)  ———–  (5)

∠ 2 = ∠ 3   (proved)

PS = PR    (sides opposite to equal angles are equal)     ———  (6)

From  (4),  (5)  and  (6) we get

PQ  =  QR  =  RS  = PS      ∴     PQRS is a rhombus.

4. PQRS is a rhombus and A, B, C and Dare the midpoints PQ, QR, RS and SP respectively. Show that the quadrilateral ABCD is a rhombus.

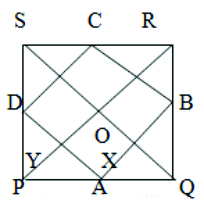
Given:  PQRS is a rhombus

A, B, C and D are the midpoints  PQ,  QR,  RS  and  SP

To prove :  The quadrilateral. ABCD is a rhombus

Proof:  Consider  Δ PRS,
C and D are the mid-points of sides  SR  and  PS  respectively

By mid-point theorem we get  CD is parallel PR  and CD =  PR    ———(1)

Now consider   Δ PRQ

A and B are the mid-points of the sides PQ and QR respectively

By mid-point theorem we get     AB is parallel to PR and AB = PR    ——–(2)

From (1) and (2) we get      CD= PR and AB= PR

From above we get CD= AB  ———–(3)

We  get      AD  =    BC          ————(4)   ( since BC = SQ  and  AD = SQ )

From (3) and (4)   we get  ABCD is a parallelogram

(ii)  (Now we have to prove that this parallelogram is a rectangle)

As  AX = YO  and  AY  =OX  we get  AXOY  is a parallelogram.

Since PQRS is a rhombus we know that the diagonals of the rhombus PR and QS bisect each other and are at right angles.So we get

∠POQ  =  ∠YOX  =  90⁰

But∠ YOX = ∠YAX = 90⁰         (opposite angles of a parallelogram)

∠YAX  =  ∠DAB  =  90⁰

Similarly we can prove that   ∠ ABC = 90⁰   , ∠ BCD = 90⁰   , ∠ CDA = 90⁰

ABCD   is a rectangle                      (proved)