8.7 TEST YOURSELF:
- Show that the diagonals of a rhombus are perpendicular to each other.
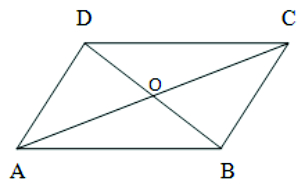
- Show that the diagonals of a square are equal and bisect each other at right angles.
- In parallelogram PQRS, two points M and N Pare taken on diagonal QS such that QN = MS.
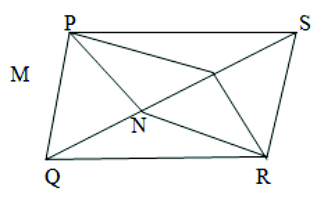
Show that : (i) PMS ≅ RNQ
(ii) PM = RN
(iii) PNQ ≅ RMS
- ABCD is a rhombus. Show that diagonal AC bisects ∠A as well as ∠C.
- In PQR and STU, PQ = ST, PQ ST= QR = UT and QR = UT. Vertices P, Q and R are joined to vertices P, Q and R respectively.
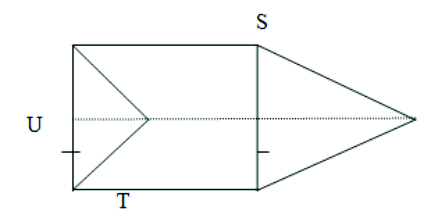
Show that (i) quadrilateral PQTS is a parallelogram.
(ii) quadrilateral PQTS is a parallelogram
(iii) PQR ≅STU
- PQRS is a rhombus and A,B,C,D are the mid-point of the sides PQ, QR, RS, PS respectively. Show that the quadrilateral ABCD is a rectangle.
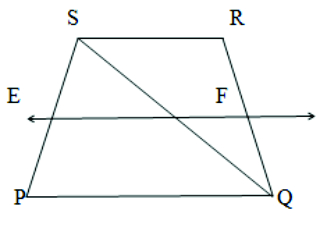
- PQRS is a trapezium in which PQ RS,QS is the diagonal and E is the mid-point of PS.
A line is drawn through E parallel to PQ intersects QR at F. Show that F is the mid-point of QR.